
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Комплексные числа
|
|
|
|
Целый ряд важных математических задач в области действительных чисел оказываются неразрешимыми. Например, квадратное уравнение с отрицательным дискриминантом в области действительных чисел корней не имеет. В связи с этим возникает необходимость соответствующего расширения множества действительных чисел. Таковым является множество комплексных чисел.
Определение 2.1. Комплексным числом называется формальное выражение вида 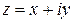 (или, что то же самое,
(или, что то же самое, 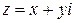 ), где х, у –любые действительные числа, а i - некоторый символ, называемый мнимой единицей. Вещественные числа х и у называются соответственно действительной и мнимой частью комплексного числа z и обозначаются символами
), где х, у –любые действительные числа, а i - некоторый символ, называемый мнимой единицей. Вещественные числа х и у называются соответственно действительной и мнимой частью комплексного числа z и обозначаются символами 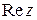 и
и 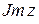 соответственно. Множество всех комплексных чисел обозначается С. Комплексное число
соответственно. Множество всех комплексных чисел обозначается С. Комплексное число 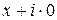 отождествляется с действительным числом х. В частности, комплексное число
отождествляется с действительным числом х. В частности, комплексное число 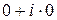 обозначают 0. Таким образом, множество действительных чисел R является подмножеством множества комплексных чисел С.
обозначают 0. Таким образом, множество действительных чисел R является подмножеством множества комплексных чисел С.
Два комплексных числа 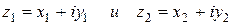 считаются равными в том и только в том случае, когда
считаются равными в том и только в том случае, когда 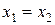 и
и 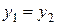 . Сумма и произведение двух комплексных чисел
. Сумма и произведение двух комплексных чисел 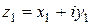 и
и 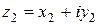 определяются формулами:
определяются формулами:
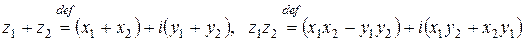 . (2.1)
. (2.1)
С помощью второй из формул (1) вычислим

Следовательно, символ 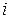 удовлетворяет условию
удовлетворяет условию 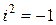 . С помощью первой из формул (2.1) легко проверить, что для каждого комплексного числа
. С помощью первой из формул (2.1) легко проверить, что для каждого комплексного числа 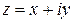 существует противоположное ему число –z такое, что
существует противоположное ему число –z такое, что 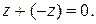 Таковым является число
Таковым является число 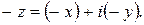 Разность двух комплексных чисел
Разность двух комплексных чисел 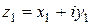 и
и 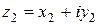 определяется формулой
определяется формулой

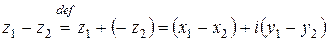 .
.
Покажем, что для каждого комплексного числа 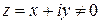 существует обратное ему число
существует обратное ему число 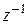 такое, что
такое, что 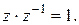 Пусть
Пусть 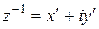 . Тогда согласно второй из формул (1) равенство
. Тогда согласно второй из формул (1) равенство 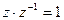 перепишется в виде
перепишется в виде
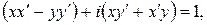
откуда по определению равенства двух комплексных чисел получаем систему уравнений для 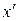 и
и 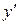
 .
.
Из этой системы находим 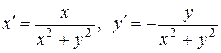 .
.
Таким образом, число 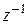 существует и выражается формулой
существует и выражается формулой
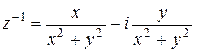 . (2.2)
. (2.2)
Частное двух комплексных чисел 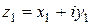 и
и 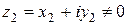 определяется формулой
определяется формулой  . Отсюда с помощью формулы (2.2) и второй из формул (2.1) для частного двух комплексных чисел получаем следующее выражение:
. Отсюда с помощью формулы (2.2) и второй из формул (2.1) для частного двух комплексных чисел получаем следующее выражение:
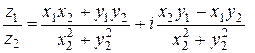 . (2.3)
. (2.3)
Комплексное число 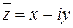 называется комплексно сопряженным к числу
называется комплексно сопряженным к числу 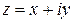 . Сумма и произведение комплексно сопряженных чисел - вещественные числа. Комплексные числа удобно изображать точками или векторами на плоскости. Если на плоскости ввести декартову прямоугольную систему координат Оху, то комплексное число
. Сумма и произведение комплексно сопряженных чисел - вещественные числа. Комплексные числа удобно изображать точками или векторами на плоскости. Если на плоскости ввести декартову прямоугольную систему координат Оху, то комплексное число 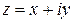 изобразится точкой М(х,у) или вектором
изобразится точкой М(х,у) или вектором  . Плоскость, на которой изображаются комплексные числа, называется комплексной. Сложение и вычитание комплексных чисел сводится к сложению и вычитанию соответствующих им векторов.
. Плоскость, на которой изображаются комплексные числа, называется комплексной. Сложение и вычитание комплексных чисел сводится к сложению и вычитанию соответствующих им векторов.
Число 
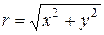 называется модулем комплексного числа
называется модулем комплексного числа 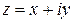 и обозначается символом
и обозначается символом 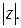 Модуль числа z равен длине вектора, изображающего это число. Всякое решение φ системы уравнений
Модуль числа z равен длине вектора, изображающего это число. Всякое решение φ системы уравнений

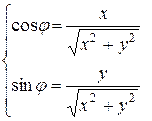 (2.4)
(2.4)
называется аргументом комплексного числа 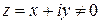 . Любые два аргумента комплексного числа отличаются друг от друга на число, кратное
. Любые два аргумента комплексного числа отличаются друг от друга на число, кратное 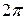 . Для обозначения аргумента комплексного числа z используется символ
. Для обозначения аргумента комплексного числа z используется символ 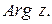 Аргумент φ, удовлетворяющий условию
Аргумент φ, удовлетворяющий условию 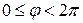 , называется главным значением аргумента и обозначается
, называется главным значением аргумента и обозначается 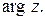 Часто главное значение аргумента определяется условием
Часто главное значение аргумента определяется условием 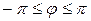 . Из формул (2.4) следует
. Из формул (2.4) следует 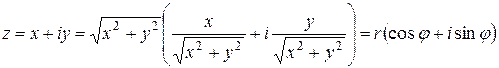 .
.
Запись 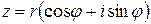 называется тригонометрической формой комплексного числа z в отличие от алгебраической формы
называется тригонометрической формой комплексного числа z в отличие от алгебраической формы 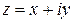 . Символом
. Символом 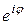 обозначается комплексное число
обозначается комплексное число 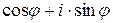 . С помощью этого символа всякое комплексное число может быть записано в показательной форме
. С помощью этого символа всякое комплексное число может быть записано в показательной форме 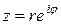 .
.
Вычислим произведение двух комплексных чисел 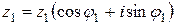 и
и 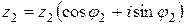 в тригонометрической форме. В силу второй из формул (2.1)
в тригонометрической форме. В силу второй из формул (2.1)
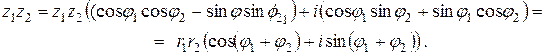
Таким образом, при перемножении комплексных чисел в тригонометрической форме их модули перемножаются, а аргументы складываются. В частности, 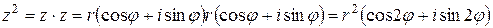 . Методом математической индукции последняя формула обобщается на случай степени с любым натуральным показателем n следующим образом:
. Методом математической индукции последняя формула обобщается на случай степени с любым натуральным показателем n следующим образом:
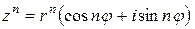 . (2.5)
. (2.5)
Это так называемая формула Муавра.
В силу (2.3) для частного двух комплексных чисел 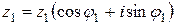 и
и 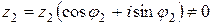 в тригонометрической форме получаем следующее выражение:
в тригонометрической форме получаем следующее выражение:
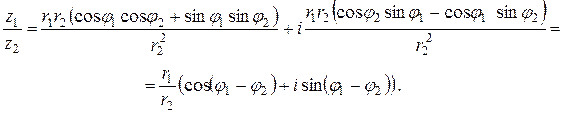
Таким образом, при делении двух комплексных чисел в тригонометрической форме их модули делятся, а аргументы вычитаются.
Займемся теперь вычислением корня из комплексного числа. По определению, корень 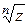 есть такое число W, что
есть такое число W, что 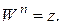 Пусть
Пусть 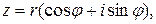 а
а  Тогда по формуле Муавра (2.5)
Тогда по формуле Муавра (2.5)
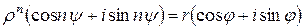 . (2.6)
. (2.6)
Из (2.6) по определению равенства комплексных чисел выводим  ,
,  ,
, 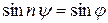 , откуда
, откуда 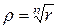 ,
, 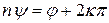 ,
, 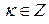 . Следовательно,
. Следовательно,
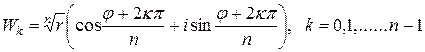 . (2.7)
. (2.7)
При остальных значениях к в силу периодичности синуса и косинуса новых значений для корня не получается. Таким образом, корень n -й степени из комплексного числа 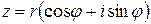 имеет ровно n различных значений, которые находятся по формуле (2.7).
имеет ровно n различных значений, которые находятся по формуле (2.7).
Пример. Вычислим  . Представим число 1 в тригонометрической форме
. Представим число 1 в тригонометрической форме 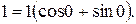 Тогда по формуле (2.7)
Тогда по формуле (2.7) 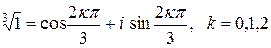 . Обозначив к -е значение корня
. Обозначив к -е значение корня  через Wk, получим три значения корня:
через Wk, получим три значения корня:
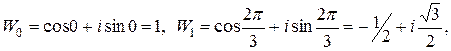
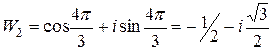 .
.
|
|
|
|
|
Дата добавления: 2014-01-14; Просмотров: 558; Нарушение авторских прав?; Мы поможем в написании вашей работы!