Формулы приближенного вычисления определенных интегралов

Приложение определенного интеграла к задачам геометрии

Вычисление площадей плоских фигур

1. В случае если отыскивается площадь криволинейной трапеции приведенной на рис. 5, когда уравнение линии ограничивающей трапецию сверху имеет вид 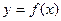, то искомая площадь 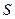определится по формуле:

.

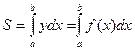2. Если связь между 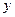и 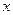задается в параметрической форме 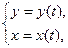то (рис. 5) площадь 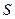определится по формуле: .

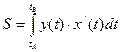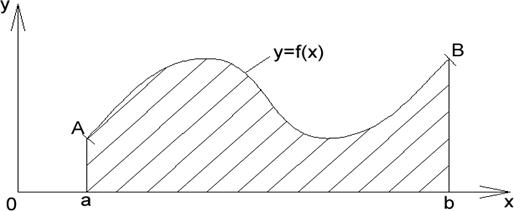
Рис. 5

2. В полярной системе координат площадь криволинейного сектора (рис. 6) определится по формуле: .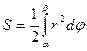

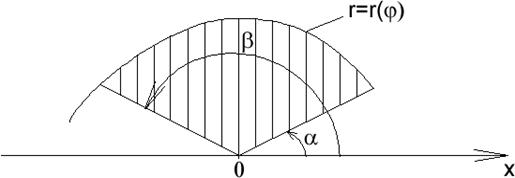
Рис. 6

Длина дуги плоской кривой

Длиной дуги кривой линии называется предел длины вписанной в эту линию ломанной, когда длина каждой стороны ломаной стремится к нулю, а число сторон ее стремится к бесконечности.

1. Если 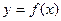- гладкая функция (непрерывная, имеющая непрерывную первую производную) (рис. 5), то длина дуги 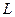на отрезке 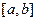определится по формуле: .

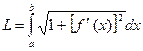2. Если связь между 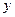и 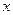задается в параметрической форме 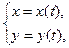то искомая .

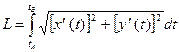3. При задании уравнения линии в полярной системе координат 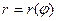(Рис. 6) искомая длина .

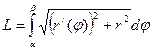Процесс отыскания длины дуги линии называется ее спрямлением.

Вычисление объема и поверхности тела

Если тело задается (Рис. 7) так, что площадь его поперечного сечения 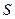плоскостью перпендикулярной оси 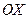есть известная функция переменной 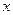, то объем этого тела 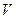определится по формуле: .

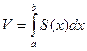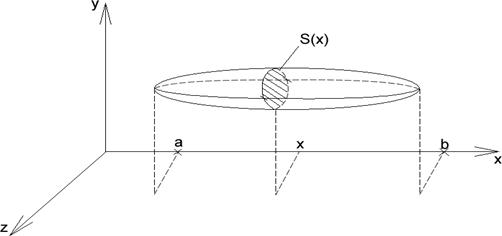
Рис. 7

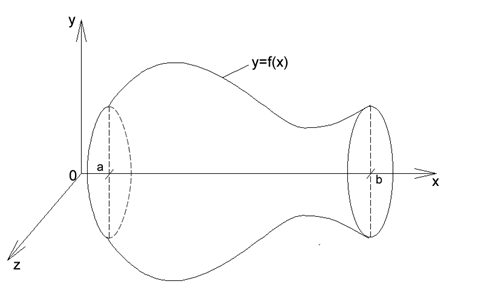
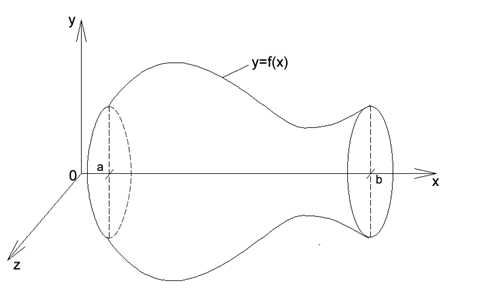Объем тела вращения линии 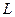- графика функции 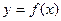вокруг оси 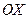на отрезке 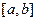(рис. 8) определится по формуле: .

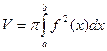Рис. 8

Поверхность тела вращения 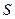в этом случае определится по формуле:

.

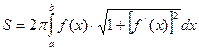Необходимость формул и методов приближенного вычисления определенных интегралов состоит в том, что с одной стороны не все интегралы можно вычислить точно (в квадратурах), с другой стороны, когда такое точное вычисление возможно, оно проводится столь громоздко, что не стоит тех затрат времени и труда которые тратятся на их отыскание. При этом часто получаемые точные решения являются «условно точными», поскольку на финише проходят через таблицы тех или иных функций и, следовательно, являются точными с точностью до точности таблиц. При приближенном же отыскании определенных интегралов вычисления часто проводятся с высокой, оцениваемой степенью точности.

Формулы прямоугольников и трапеций

Здесь интервал интегрирования 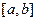разбивается на n равных частичных интервалов длиной 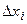точками 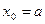, , 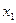,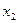…, 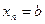и тогда функция 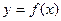в точках деления интервала будет принимать значения 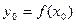, , 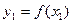,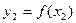…, ,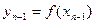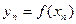(рис. 9).

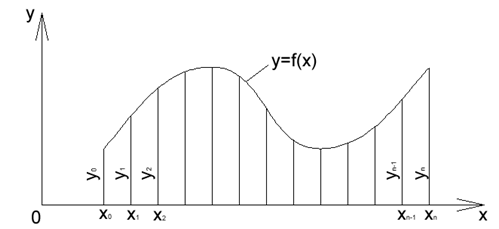
Рис. 9

Теперь

, .

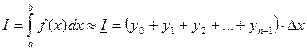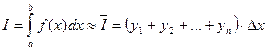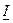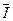Формулы для вычисления и - формулы прямоугольников. Формула трапеций отсюда

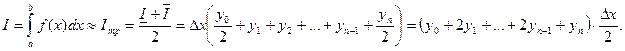В общем случае формула трапеций более точна, чем формулы прямоугольников.

Формула Симпсона

При приближенном вычислении определенного интеграла по формулам прямоугольников искомая площадь заменяется площадью некоторой столбчатой фигуры. При вычислении по формуле трапеций, искомая площадь заменяется площадью фигуры, ограниченной сверху хордами, стягивающими дуги кривой 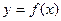на частичных интервалах. В случае формулы Симпсона интервал интегрирования 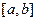разбивается на четное количество 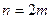частичных интервалов и на каждом сдвоенном интервале дуга кривой 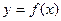заменяется дугой параболы проходящей через три точки. Формула Симпсона приближенного вычисления определенного интеграла имеет вид:

Формула Симпсона дает более точные значения для определенного интеграла, чем формулы прямоугольников и формула трапеций. Позже, при изучении темы «Ряды» мы возвратимся к вопросу приближенного вычисления определенных интегралов.

Дата добавления: 2014-01-14