
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Несобственные интегралы. Согласно теореме существования определенный интеграл существует, если выполняются два условия:
|
|
|
|
Согласно теореме существования определенный интеграл  существует, если выполняются два условия:
существует, если выполняются два условия:
1) [ a, b ] – конечный интервал; 2)  - непрерывная функция.
- непрерывная функция.
Если же одно из отмеченных условий не выполняется, то говорить об определенном интеграле как о пределе n - ой интегральной суммы мы не можем, поскольку такой предел может не существовать. В этом случае мы имеем дело с так называемыми несобственными интегралами. Различают несобственные интегралы с бесконечными пределами и несобственные интегралы от разрывных функций.
Несобственные интегралы с бесконечными пределами
Несобственным интегралом от функции 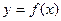 на интервале [ a,
на интервале [ a,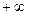 )называется предел интеграла
)называется предел интеграла при
при  :
: 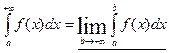 .
.
Если при этом подчеркнутый предел существует, то говорят, что несобственный интеграл  - сходится. В противном случае говорят, что несобственный интеграл расходится.
- сходится. В противном случае говорят, что несобственный интеграл расходится.
Если 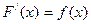 , то схема отыскания несобственного интеграла следующая:
, то схема отыскания несобственного интеграла следующая: 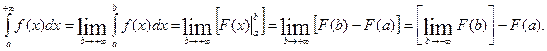
Интегралы 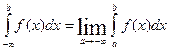 и
и
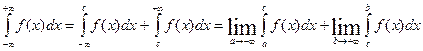 находятся аналогично.
находятся аналогично.
Геометрический смысл несобственного интеграла
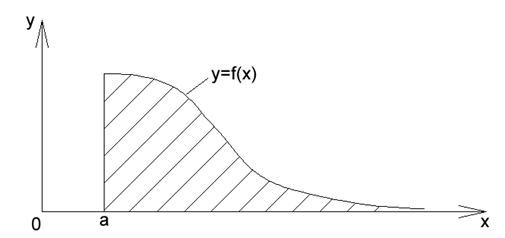 Если несобственный интеграл
Если несобственный интеграл  сходится, то можно говорить, что заштрихованная (бесконечная вправо) фигура (Рис. 10) имеет площадь равную этому интегралу.
сходится, то можно говорить, что заштрихованная (бесконечная вправо) фигура (Рис. 10) имеет площадь равную этому интегралу.
Рис. 10
Если же интеграл расходится, то говорить о площади фигуры нельзя.
Признаки сходимости – расходимости
Часто бывает достаточно установить сходится рассматриваемый несобственный интеграл или расходится и в случае сходимости оценить его значение. Эти обстоятельства помогают выяснить следующие признаки сравнения.
1. Если 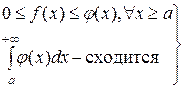
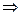
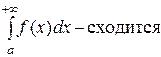
и при этом 
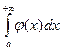 .
.
2. Если 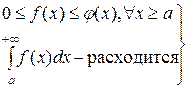
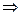
 .
.
Эти свойства нетрудно понять из рис. 11.

Рис. 11
Несобственные интегралы от разрывных функций
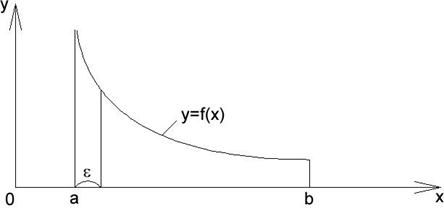
Если 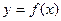 - непрерывная функция для всех
- непрерывная функция для всех 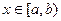 и
и 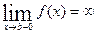 (рис. 12), то
(рис. 12), то 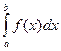 - несобственный интеграл, который определяется, как предел интеграла
- несобственный интеграл, который определяется, как предел интеграла 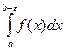 (
(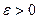 ) при
) при  :
:
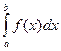
 .
.
При этом если предел, стоящий в правой части последнего соотношения, существует и конечен, то говорят, что рассматриваемый несобственный интеграл сходится. В противном случае интеграл расходится.

Рис. 12
Если  , то схема вычисления рассматриваемого несобственного интеграла следующая:
, то схема вычисления рассматриваемого несобственного интеграла следующая:
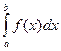
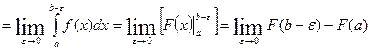 .
.
 Аналогично, если
Аналогично, если 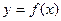 - непрерывная функция для всех
- непрерывная функция для всех 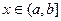 и
и  (Рис. 13), то
(Рис. 13), то 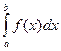 - несобственный интеграл.
- несобственный интеграл.
Рис.13
В этом случае: 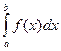
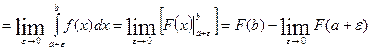 .
.
В случае же, когда 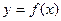 - непрерывна для
- непрерывна для 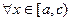 и
и 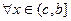 и
и  , то
, то 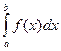 - несобственный интеграл, который вычисляется по следующей схеме:
- несобственный интеграл, который вычисляется по следующей схеме: 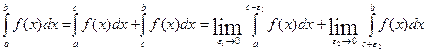 .
.
Признаки сходимости здесь можно записать по аналогии с признаками сходимости для интеграла с бесконечными пределами.
П р и м ер. Вычислить несобственный интеграл  , где
, где  - любое действительное число, или доказать что он расходится.
- любое действительное число, или доказать что он расходится.
Р е ш е н и е.

Таким образом, рассматриваемый несобственный интеграл I расходится при  и сходится при
и сходится при  .
.
П р и м е р. Вычислить несобственный интеграл 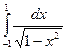 или доказать что он расходится.
или доказать что он расходится.
Р е ш е н и е.
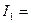
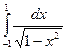 =
=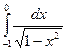 +
+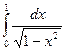 =
=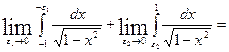
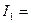
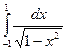 =
=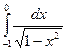 +
+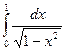 =
=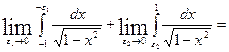
=
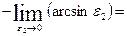
 .
.
Таким образом, рассматриваемый несобственный интеграл  сходится и равен
сходится и равен  .
.
|
|
|
|
Дата добавления: 2014-01-14; Просмотров: 555; Нарушение авторских прав?; Мы поможем в написании вашей работы!