Криволинейные инт. 2 рода (интегралы по координатам)

Определения и вычисление. Векторным полем в области 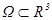наз. правило 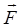, которое ставит в соответствие вектор 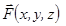с началом в точке . определяет координатные функции

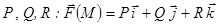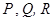, заданные в Ω. наз. непр. если непр. и наз. гл. если 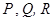имеют непр. частные производные.

Пр. – поле радиуса вектора.

Гл. кривая Γ в 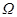наз. ориентированной, если указано направление ее обхода. Пусть 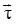непр. поле единичных касательных векторов, согласованное с направлением обхода. Такое поле имеет "гл. кривая и наз. направлением.

Криволинейным интегралом 2-го рода от поля по кривой Γ в направлении 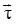наз. число 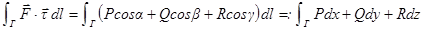, где последнее выражение является обозначением. Отметим, что такие интегралы можно определить с помощью предела интегральных сумм второго типа, , ,

,

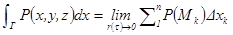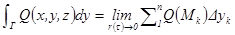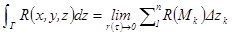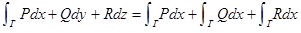
Сведем все к определенному интегралу регулярной параметризацией

, пусть ,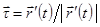

тогда получаем схему вычислений

.

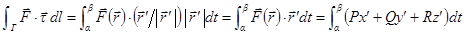В частности в пространстве ,

на плоскости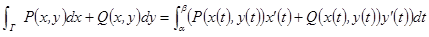

Пр.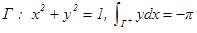

Интеграл второго рода дает работу сил поля вдоль заданного пути.

Свойства интегралов второго рода ( )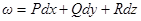

1. При переходе к противоположному направлению инт. меняет знак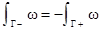

2. Если кривая Γ разделена точкой на две части 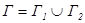, тогда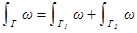

Дополнение к определению: если кривая Γ кусочно-гладкая, и их направления согласованы в т. соединения, то по опр. .

Формула Грина. Пусть (1) P и Q непр. диф. в области ,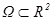

(2) 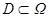- допустимое множество, граница которого Γ- простой кусочно-гладкий контур Þ .

Приложение к геометрии, вычисление площади с помощью интеграла второго рода: .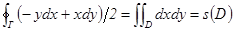

Пр.: площадь эллипса.

Независимость инт. от формы кривой в R². Пр. 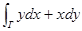не зависит от формы кривой, а 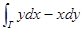зависит.

Пусть P и Q гл. фун в односвязной области 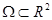, следующие условия равносильны

1) 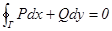" кусочно-гладкого контура ;

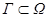2) 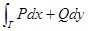не зависит от формы Γ;

3) ;

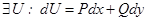4) 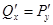в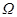



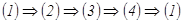
Зам.: фун U наз. потенциалом поля 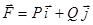, а 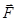 потенциальным, вектор 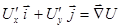наз. градиентом U, поле 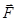будет потенциальным, если 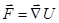для некоторого потенциала U. Условие односвязности 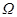существенно, контр пример: 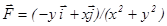в 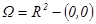не потенциально, хотя .

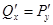Дата добавления: 2014-01-14