
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тройные интегралы
|
|
|
|
Определения. Пусть f опред. и огранич в паралл A, τ -разбиение A на n паралл, их объемы и диаметры = 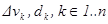 , в" паралл. выберем т
, в" паралл. выберем т 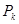 и образуем сумму
и образуем сумму 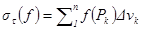 . Введем ранг τ:
. Введем ранг τ: 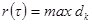 и определим предел интегральных сумм:
и определим предел интегральных сумм:
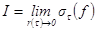 , если
, если 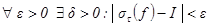 как только
как только  независимо от
независимо от
выбора 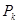 .
.
Тройным интегралом от f по A наз. число  , если предел существует, при этом f наз интегрируемой функцией по A.
, если предел существует, при этом f наз интегрируемой функцией по A.
Далее, множество  имеет нулевой объем, если его можно покрыть конечным числом параллелепипедов, сумма объемов которых сколь угодно мала.
имеет нулевой объем, если его можно покрыть конечным числом параллелепипедов, сумма объемов которых сколь угодно мала.
Пр., график непр. функции двух переменных на ограниченном и замкнутом множестве, гладкая поверхность имеют нулевой объем.
Признак инт.: если  имеет нулевой объем, а f непр. в
имеет нулевой объем, а f непр. в 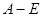 , то f инт. по A.
, то f инт. по A.
Далее, множ. 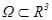 наз. допуст. если оно ограничено, замкнуто и его граница имеет нулевой объем. Определим тр. интеграл по такому множ. Пусть f непр. на допуст. множ. Ω, тогда $ параллелепипед AÉ Ω, определим
наз. допуст. если оно ограничено, замкнуто и его граница имеет нулевой объем. Определим тр. интеграл по такому множ. Пусть f непр. на допуст. множ. Ω, тогда $ параллелепипед AÉ Ω, определим 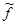 :
: 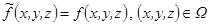 ,
, 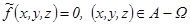 , она инт. по A, ее точки разрыва имеют нулевой объем, положим по опред.
, она инт. по A, ее точки разрыва имеют нулевой объем, положим по опред.  .
.
Пр. 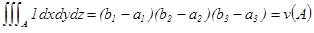 ;
; 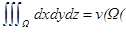 -объем Ω по опред.
-объем Ω по опред.
Свойства
1 Линейность 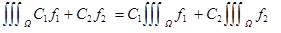
2 Аддитивность. Пусть Ω разделена поверхностью на 2 части 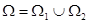 , тогда
, тогда 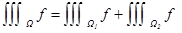
3 Монотонность. 1) 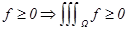 , 2)
, 2) 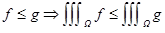 , 3)
, 3) 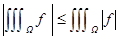
4 Т. о среднем значении. Пусть f непр. на допуст. множ Ω, тогда  ,
, 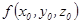 наз. ср. знач. f на Ω.
наз. ср. знач. f на Ω.
Вычисление
1 Повторные интегралы. Это конструкции вида 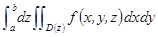 или
или 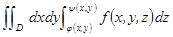
Пр. 1) 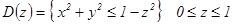 Þ
Þ 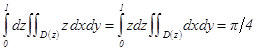
2) 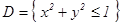 ,
, 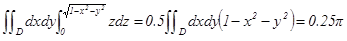
2 Прав допуст множ. Пусть функции 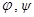 непрерывны на замкнутом и ограниченном множестве D с кусочно-гладкой границей и
непрерывны на замкнутом и ограниченном множестве D с кусочно-гладкой границей и 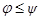 на D.
на D.
Множ 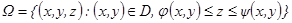 наз. правильным вдоль OZ.
наз. правильным вдоль OZ.
3 Т. Фубини о сведении тройного интеграла к повторному. Пусть множ Ω прав вдоль OZ, опред функциями 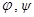 , а f непр в Ω, тогда
, а f непр в Ω, тогда 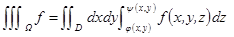 .
.
Пр. 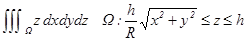
Приведем еще одну конструкцию повторного интеграла, к которому сводится тройной интеграл. Пусть Ω занимает вдоль Z отрезок [a,b] и сечения D(z) – допуст. множ, тогда 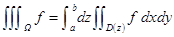 , если $ внутренний двойной инт. по сечениям.
, если $ внутренний двойной инт. по сечениям.
Приложение
1) Масса тела 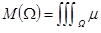 , объем
, объем 
2) Ст. моменты и ц. м. трехмерной фигуры
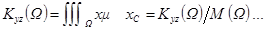
3) Моменты инерции трехмерной фигуры относительно осей координат 
|
|
|
|
Дата добавления: 2014-01-14; Просмотров: 459; Нарушение авторских прав?; Мы поможем в написании вашей работы!