
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные понятия. 1 Пространство исходов. Испытанием называется определенная последовательность действий, которую можно воспроизвести любое число раз
|
|
|
|
1 Пространство исходов  . Испытанием называется определенная последовательность действий, которую можно воспроизвести любое число раз. Оно называется случайным, если его результат невозможно предсказать. Цель испытания – изучение некоторой системы или явления.
. Испытанием называется определенная последовательность действий, которую можно воспроизвести любое число раз. Оно называется случайным, если его результат невозможно предсказать. Цель испытания – изучение некоторой системы или явления.
Всякое свойство системы, которое можно обнаружить или не обнаружить в результате случайного испытания наз событием.
Среди всех событий выделяют множество 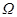 – элем событий, его называют пространством исходов, которые отвечают требованию: непременно наступает одно и только одно из них. Кроме того, для каждого события
– элем событий, его называют пространством исходов, которые отвечают требованию: непременно наступает одно и только одно из них. Кроме того, для каждого события  и любого исхода
и любого исхода 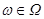 должно быть известно влечет исход ω наступление
должно быть известно влечет исход ω наступление  или нет. Если да, то ω наз благоприятствующим
или нет. Если да, то ω наз благоприятствующим  , и это выражают в виде
, и это выражают в виде  иначе
иначе 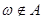 , т.о. всякое событие является частью
, т.о. всякое событие является частью 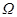 ,
, 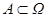 .
.
2 Алгебра событий. События можно складывать, умножать и переходить к противоположному событию.
1) Суммой событий  и
и 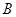 наз. событие
наз. событие 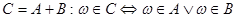 ;
;
пусть 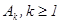 – последовательность событий, их суммой наз. событие
– последовательность событий, их суммой наз. событие 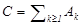 , которое наступает тогда, когда наступает хотя бы одно из событий послед,
, которое наступает тогда, когда наступает хотя бы одно из событий послед, 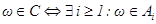 .
.
2) Произведением  и
и 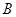 наз. событие
наз. событие 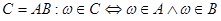 ;
;
3) Противоположным событием к A наз. событие 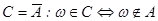 ;
;
4) 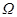 тоже событие, оно наз достоверным событием;
тоже событие, оно наз достоверным событием;
5) Невозможным наз событие, которое никогда не наступает, его обозначают символом  ;
;
6) События A и B наз несовместными событиями если  .
.
Существует масса формул, которые связывают эти операции:
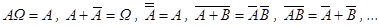
Имеется тесная связь между операциями над событиями и множ.
Пусть  некоторый класс событий,
некоторый класс событий,  наз алгеброй если
наз алгеброй если
1) 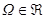 ; 2)
; 2)  ; 3)
; 3) 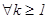
 .
.
В частности,  , если
, если  , т.к.
, т.к. 
3 Вероятностью на алгебре  наз. правило P, которое
наз. правило P, которое  ставит в соответствие число
ставит в соответствие число 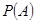 и удовлетворяет следующим условиям
и удовлетворяет следующим условиям
1)  2)
2) 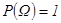 3)
3)  , если
, если 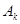 попарно несовместные события.
попарно несовместные события.
В частности, 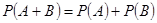 если
если  .
.
Тройка 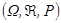 наз вероятностным пространством.
наз вероятностным пространством.
Из указанных условий получаем два утверждения:
1. 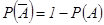
· 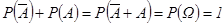
2. 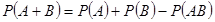
·  ,
, 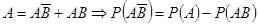
Следствие. 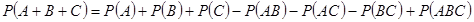
4 Вычисление вероятности
Классическая схема: если 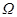 −конечное и все исходы одинаково возможны, тогда
−конечное и все исходы одинаково возможны, тогда 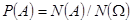 , где
, где 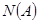 – число исходов, которые приводят к наступлению A, а
– число исходов, которые приводят к наступлению A, а 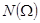 – число всех исходов. При решении задач на КС используют комбинаторные формулы. Каждая такая формула определяет общее число исходов в некотором опыте, состоящем в выборе наудачу m элем из n различных элементов исходного множества. При этом оговаривается (1) способ выбора и (2) что следует понимать под различными выборками. Существуют 2 схемы выбора, с возвращением и без него. Кроме того выбранные элементы могут быть упорядочены или нет. Получаем 4 конструкции.
– число всех исходов. При решении задач на КС используют комбинаторные формулы. Каждая такая формула определяет общее число исходов в некотором опыте, состоящем в выборе наудачу m элем из n различных элементов исходного множества. При этом оговаривается (1) способ выбора и (2) что следует понимать под различными выборками. Существуют 2 схемы выбора, с возвращением и без него. Кроме того выбранные элементы могут быть упорядочены или нет. Получаем 4 конструкции.
1.Опыт состоит в выборе m элементов без возвращения и без упоряд, исходы различаются составом элементов. Комбинации такого сорта наз. сочетаниями из n элем по m, их общее число  .
.
Пр. (14.79, 14.83, 14.84)
2.Выбор m элементов без возвр, но с упорядочиванием по мере выбора, исходы различаются составом элементов или порядком их следования. Такие комбинации наз размещениями из n элем по m, их общее число  . При равенстве
. При равенстве 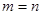 получаем
получаем  , и опыт состоит в выборе случайной перестановки.
, и опыт состоит в выборе случайной перестановки.
Пр. (14.90, 14.91, 14.97)
3.Выбор m элем с возвр, но без упоряд, исходы различаются составом элементов, которые могут повторяться. Такие исходы наз сочетаниями с повторениями, их общее число  .
.
Пр. (14.98)
4.Выбор m элем с возвр. и с упоряд. по мере выбора, исходы различаются составом или порядком следования. Такие комбинации наз размещениями с повторениями, их общее число 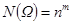 .
.
Пр. (14.100)
Геометрические вероятности: если Ω можно представить в виде множества DΩ Ì R2, и каждая точка DΩ одинаково возможна, тогда P(A)=S(DA)/S(DΩ) – отношение площадей.
Пр.: задача Бюффона Пр. (14.148, 14.143, 14.154)
|
|
|
|
Дата добавления: 2014-01-14; Просмотров: 377; Нарушение авторских прав?; Мы поможем в написании вашей работы!