Условные вероятности и независимость

1 Определение. Условной вероятностью A по отношению к B наз число . В классическом случае:

Пр. из урны, содержащей 2 белых шара и 1 черный, последовательно вынимают 2 шара, вычислить вероятность того, что второй белый при условии, что первый тоже белый.

На самом деле вероятность события . С помощью условных вер выражается вероятность произведения событий:

, ,...,

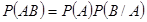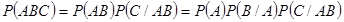вероятность произведения = произведению условных вероятностей.

2 Формула полной вероятности. Набор событий 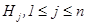наз. полной группой, если они попарно несовместны, а их сумма достоверное событие.

Теорема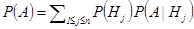

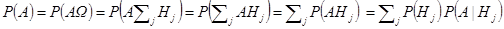
3 Формула Байеса. Пусть 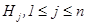полная группа, и произошло событие A, тогда можно вычислить условные вероятности:

.

Формула позволяет переоценить гипотезы после наступления события .

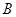4 Независимость. События A и B наз. незав. если . Отсюда получаем , т.е. наступление не меняет вероятности .

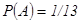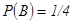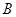Пр.: из колоды карт в 52 листа вынимают одну карту, пусть A=(дама), B=(пика), тогда , , , поэтому и независимые, так устроены карты!

Задача: если и 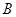незав., то противоположные к ним события тоже незав., док.

Опр. События 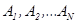наз. незав. в совокупности если

для всякого поднабора .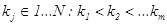

Пр.: из незав. любых двух не следует незав. в совокупности, игральная кость в форме тетраэдра и три краски.

Схема Бернулли повторения испытаний

Пусть p – вер события A в одном испытании и n>1, схемой Бернулли наз. серия из n независимых испытаний: вероятность события A в каждом испытании не зависит от исходов других испытаний. Свяжем с этой серией набор из 1 и 0 в

зависимости от наступления или нет события A, и припишем такому набору вероятность , где m – число единиц в наборе. Такая вероятность выражает независимость испытаний в серии. Часто единицу наз успехом, а нуль неудачей. Распределение числа успехов дает выражение .

Приближенные соотношения в схеме Бернулли:

1) Формула Пуассона , ( или )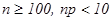

2) Локальная формула Муавра – Лапласа,

.

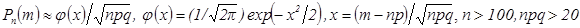3) Интегральная формула Муавра – Лапласа , , ( ).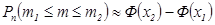

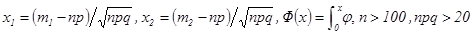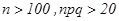Пр.1: игральная кость бросается 12000 раз, найти вер того что число выпадений тройки будет заключено между 1900 и 2150,

.

Пр.2: сколько раз надо бросить монету, чтобы с вероятностью 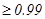, частота появления герба отличалась от вер 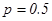не больше чем .

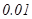Пусть , найдем наименьшее число испытаний n из условия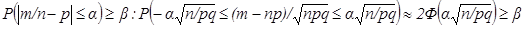

.

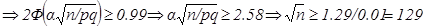Пр.3: вер попадания в цель 0.1, сделано 100 выстрелов, в каких пределах с вер. 0.8, будет лежать относительная частота попаданий.

Пусть 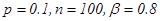найдем из уравнения , , .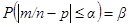

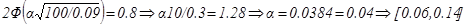Случайные величины и их распределения.

1 Определения. Пусть 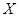фун, заданная на 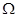, 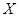наз СВ если 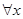прообраз является событием и имеет некоторую вер, при этом выражение наз функцией распределения (ФР) СВ .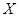

Пр.: точку наудачу бросают внутрь круга радиуса R, вер. попадания ее в любую часть круга пропорциональна площади этой части. Обозначим через 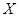расстояние точки до центра круга. Найти ФР СВ .

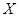2 Свойства ФР.

1)

2) F не убывает

3)

4) F непр. слева

5)

· 3) ,

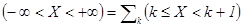
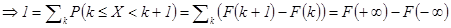
3 Дискретные случайные величины. Случайная величина 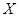наз дискретной, если ее множество значений конечное или счетное. Пусть 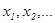значения 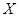, , 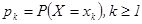тогда сумма 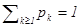. Множество всех пар наз. РР 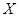.ДСВ часто задается своим рядом распределения.

Пр.: проводится тестирование деталей, произведенных автоматом; вер., что деталь ст. = 0.9; тестирование проводится до 1−го появления ст. детали; пусть 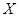число проверенных деталей; построить РР .

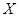Функцию распределения ДСВ можно представить в виде суммы накопленных вероятностей отсюда следует, что

1) график F имеет ступенчатую форму,

2) F возрастает скачками в точках ,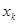

3) величина скачка равна ,

4) ,

4 Непрерывные случайные величины. 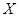наз непрерывной если ее функция распределения выражается интегралом 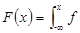, 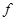наз плотностью распределения 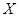, будем считать ее кусочно-непрерывной.

Свойства функции плотности: 1) и в точках непр, 2) ,

3) .

НСВ часто задается плотностью распределения.

Дата добавления: 2014-01-14