Моменты. Дисперсия. Среднее квадратичное отклонение

Опр. Начальным моментом S –го порядка с. в. Х называется мат. ожидание S^ой степени этой величины:

Или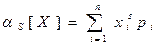

А для непрерывной с. в.:

Мат. ожидание - есть начальный момент первого порядка.

Опр. Центрированной с. в. называется отношение с. в. от её мат. ожидания: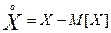

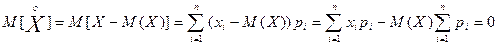
Опр. Центральным моментом порядка S с. в. Х называется мат. ожидание S-ой степени центрированной с. в.:

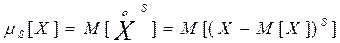
Для дискретной с. в.:

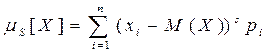
Для непрерывной с. в.:

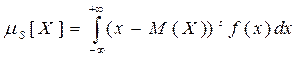
Центральный момент первого порядка:

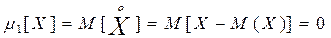
Второго порядка:

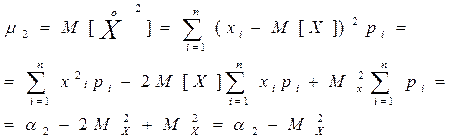
Третьего порядка:

Аналогично: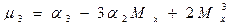

Опр. Дисперсией с. в. есть мат. ожидание квадрата соответствующей центрированной величины: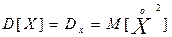

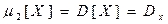
Для дискретной с. в.: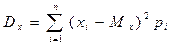

Для непрерывной: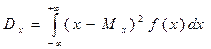

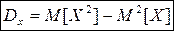
Замечание:

Дисперсия есть характеристика рассеивания, разбросанности с. в. около её мат. ожидания.

Опр. Средним квадратичным отклонением с. в. называется величина, равная квадратному корню из дисперсии:

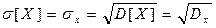
Третий центральный момент характеризует асимметрию распределения:

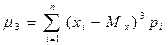
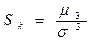- коэффициент асимметрии.

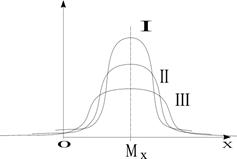
Четвёртый центральный момент m₄ служит характеристикой крутости.

Эксцесс:

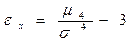
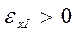
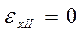
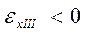
Свойства мат. ожидания и дисперсии.

1) I) Математическое ожидание неслучайной величины С равно самой величине С:

М [С] = С

II) Дисперсия неслучайной величины С равна нулю:

D [C] = 0

2) I) При прибавлении к с.в. Х неслучайной величины С к её мат. ожиданию прибавляется та же величина:

M [ X+C] = M [ X ] + C

II) а её дисперсия не меняется:

D [ X+C ] = D [ X ]

3) I) При умножении с. в. Х на неслучайную величину С на ту же величину С умножается её мат. ожидание:

M [ C*X ] = C*M[ X ]

II) Дисперсия умножается на С²:

D [ C*X ] = C² M [ X ]

Глава 5 Некоторые важные для практики распределения дискретных с. в.

Дата добавления: 2014-01-14