Биноминальное распределение

Испытания Бернулли.

Опр. Повторные независимые испытания называются испытаниями Бернулли, если каждое испытание имеет только два возможных исхода и вероятности исходов оказываются неизменными для всех испытаний.

Обозначим эти вероятности через p и q, и пусть p – «успех» - У

q – «неудача» –Н

Очевидно: p+q =1

Пространство элементарных событий отдельного испытания состоит из двух точек, а n испытаний - из 2ⁿ точек.

Вероятность любой последовательности есть произведение, полученное при замене символов У и Н на p и q соответственно, т. е.

Р{УУНУН … ННУ} = ppqpq … qqp

Опр. Дискретная случайная величина Х имеет биноминальное распределение, если её возможные значения: 0,1,…, m, …,n,а соответствующие вероятности: P_m=P{X=m} = C_n^m p^mq^n-m

где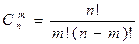

а 0<p<1; q=1-p; m = 0,1, …,n

Теорема: если с. в. Х есть количество успехов в n испытаниях Бернулли, то оно имеет биноминальное распределение:

Док-во:

Пусть произведено n испытаний Бернулли.

Необходимо найти вероятность P_m (события -m успехов)

B₁={УУ…У Н…Н }

123 123

m (n-m) раз

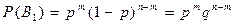
Точно такую же вероятность имеют и все варианты с m успехами и n-m неудачами.

Число таких вариантов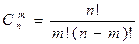

т.е.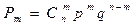

P₀ = qⁿ P_n= P{++…+ } =pⁿ

Если задача ставится как: «не менее m успехов в n опытах», то

R_m=P{x³m}=P{x=m}+P{x=m+1}+…+P{x=n}

Þ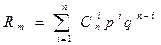

или

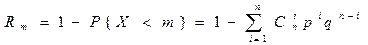
Числовые характеристики биноминального распределения:

Производящая функция:

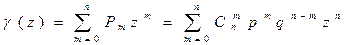
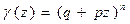
Мат. ожидание: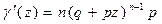

Принимая здесь z=1

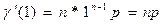т.е. M_x = np

Второй начальный момент:

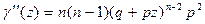
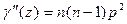
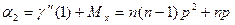
Дисперсия:

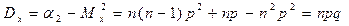
Среднее квадратичное отклонение:

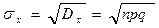
Дата добавления: 2014-01-14