F-распределение и проверка гипотезы о равенстве дисперсий двух нормальных генеральных совокупностей

Гипотезы о дисперсиях имеют особенно большое значение в технике, т.к. измеряемая дисперсией величина рассеивания характеризует такие исключительно важные показатели, как точность машин и приборов, точность технологических приемов и т. д.

Формулировка задачи:

X и Y подчиняются нормальному закону распределения

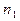и объёмы выборок из X и Y

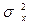и дисперсии выборок из X и Y

Оценкой 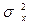является 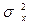, а -

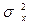
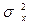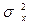Опр. Совместный закон распределения статистик и является F-распределением, или распределением Фишера – Снедекора.

Если справедливо, то:

Выбрав вероятность p=1-и по таблице определяем критическое значение

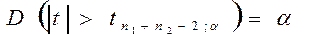
Вывод: Если вычисленное значение 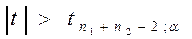,то с надёжностью p=1-можно считать расхождение средних значимым (неслучайным)

Рассмотрим случ. величину V – нормально распределённую с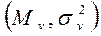

Произведем две независимые выборки с объёмам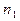и и

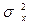Для оценки можно использовать и

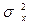
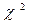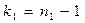Случайные величины и - распределены по закону с и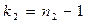

Опр. Случайная величина определяемая отношением

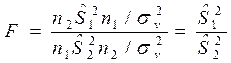
называется случайной величиной с распределением Фишера - Снедекора.

Существуют таблицы для F – распределения в которых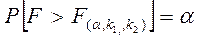

Возвращаемся к задаче :

Выбрав уровень значимости по таблице F – распределения находим

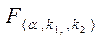
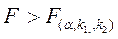- критическая область

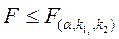- область допустимых значений

10.5 Проверка гипотез о законе распределения. Критерий согласия .

Во многих практических задачах точный закон распределения используемой случайной величины неизвестен, т.е. является гипотезой, которая требует статистической проверки.

Х – исследуемая случ. величина.

- X подчиняется закону распределения F(x).

Проводим выборку из n независимых наблюдений.

Строим эмпирическое распределение F*(x)

Сравнение эмпирического F*(x) и теоретического распределений производится с помощью специально подобранной случайной величины - критерия согласия.

Примеры: Пирсона, Колмогорова, Смирнова и др.

Наиболее часто употребим критерий согласия .

Разобьем всю область изменения Х на L интервалов.

- количество элементов, попавших на i-ый интервал

По закону распределения F(x) можно определить {вероятность попадания Х на}

- теоретическое количество элементов, попавших на

		…
		…
		…

- ()

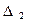
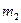
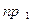
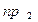
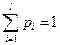
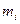
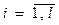Если верна, то {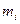} подчиняется биноминальному закону.

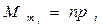
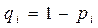
При -а 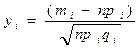распределена нормально

Доказательство:

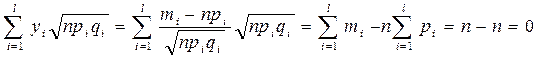
В литературе доказывается, что:

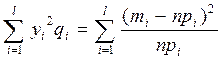- имеет распределение с k=(n-1)

Величина при имеет распределение с k=(l-r-1)

(r - число параметров распределения F(x))

Следовательно, в качестве меры расхождения между 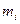и для 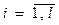используется критерий:

=

Правило применения критерия .

Выбрав уровень значимости , по таблице определяем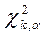

Если > 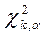, то отвергается

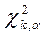< , то принимается

10.6 Вычисление объёма выборки.

После того как для оценки интересующего параметра генеральной совокупности обоснованно выбран способ образования выборки, приступают к расчету необходимого объёма выборки, задавшись желаемой степенью точности оценки 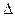и доверительной вероятностью .

Рассмотрим случайную выборку с возвратом:

Х – нормально распределена

- известна

Интервал мат. ожидания:

Длина доверительного интервала:

Длина доверительного интервала определяет точность параметра

откуда

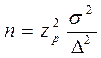
Если неизвестна, то предварительно берут небольшую пробную выборку и по её данным делают приближенную оценку параметра .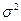

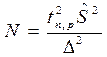
где - выборочная дисперсия пробной выборки

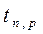- число, взятое из таблицы, соответствующее вероятности p и числу наблюдений n.

Глава 11 Основы дисперсионного анализа.

Дата добавления: 2014-01-14