КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 7. Во всех случаях, когда важно получить требуемое качество движения второй массы, а также при регулировании ее координат
|
|
|
|
Во всех случаях, когда важно получить требуемое качество движения второй массы, а также при регулировании ее координат, пренебрегать влиянием упругостей механических связей нельзя.
Речные наносы, их образование и характеристики. Твердые частицы, транспортируемые водой, принято называть наносами. Наносы состоят из минеральных зерен различной крупности. В состав наносов могут входить также частицы органического происхождения. Количество наносов проносимых через живого сечения потока в единицу времени, называют расходом наносов. Общее количество наносов, проносимые водотоком за определенный промежуток времени, например за год, называется твердым стоком.
Лекция № 5.
Содержание: Водная эрозия. Речные наносы, их образование и характеристики Взвешенные наносы. Измерение расхода и стока взвешенных наносов.
Водная эрозия. Процесс разрушения и отложения почвогрунта и горной породы под воздействием дождя и движущейся воды называют водной эрозией. Различают эрозию склоновую и русловую. Эрозия сопровождается процессом аккумуляции (накопления) наносов и продуктов разрушения в понижениях рельефа, русловой сети, водохранилищах и др. Поэтому эрозионно-аккумулятивные явления рассматриваются как единый процесс. Сопротивляемость почвогрунта размыву зависит от его исходной влажности, наличия дернового покрова, который ослабляет склоновую эрозию.
Водный поток, транспортирующий наносы является двухфазным, т.к. он состоит из жидкой и твердой фазы.В зависимости от формы передвижения потоком наносов различают взвешенные и влекомые (или донные) наносы. Взвешенные наносы - это мелкие минеральные частицы, переносимые потоком во взвешенном состоянии. Наносы перемещаемые водным потоком в придонном слое скольжением, перебрасыванием (сальтация) или перекатыванием называют влекомыми наносами. Донные наносы состоят из более крупных частиц, чем взвешенные. Чем больше скорость потока, тем более крупные частицы могут переходить во взвешенное состояние. Твердый сток реки может быть определен в полном объеме только в результате учета всех категорий наносов и растворенных веществ. При гидрометрических измерениях отдельно учитывают расход взвешенных наносов, расход донных наносов и расход растворенных веществ (кг/с).
В зависимости от участия наносов в формировании русел и их элементов различают руслоформирующие и транзитные наносы. На равнинных реках к руслоформирующим относят наносы с размерами частиц крупнее 0,05 мм.
Для оценки степени насыщения потока наносами используют понятие мутность воды. Количество наносов в граммах, содержащееся в 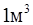
 воды, называется мутностью, или же мутность это отношение количества наносов (в единицах массы или объемных единицах) к объему смеси воды с наносами.
воды, называется мутностью, или же мутность это отношение количества наносов (в единицах массы или объемных единицах) к объему смеси воды с наносами.
Если объемный расход двухфазного потока (м3/с)
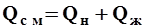 (1) (1)
| (1) |
где 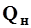 - объемный расход твердой фазы (наносов), м3/с;
- объемный расход твердой фазы (наносов), м3/с; 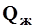 - объемный расход жидкой фазы (воды), м3/с; и при
- объемный расход жидкой фазы (воды), м3/с; и при 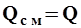 , тогда объемная относительная мутность выразится отношением
, тогда объемная относительная мутность выразится отношением 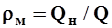 . Массовый расход взвешенных наносов
. Массовый расход взвешенных наносов 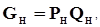 , где PН-плотность наносов.
, где PН-плотность наносов.
Средняя массовая мутность всего потока
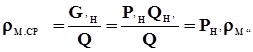 (2) (2)
| (2) |
Кроме расходов и стока наносов и мутности, различают модуль стока наносов - количество наносов в тоннах с 1 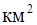 за од т/(км2.год). за од т/(км2.год).
|
Водный поток транспортирует наносы различной крупности и формы. В гидрометрии принято подразделять наносы по размеру частиц. За размер частиц принимают ее средний диаметр. Имеется классификация речных наносов по размеру частиц. Кроме классификации наносов по размеру частиц применяют еще деление их по гидравлической крупности.
Гидравлической крупностью называется скорость равномерного падения частиц в неподвижной водной среде. Гидравлическая крупность измеряется в сантиметрах в секунду или в миллиметрах в секунду. В таблице 1 приведены значения гидравлической крупности частиц при температуре 15°С.
Таблица 1.
| Диаметр частицы, мм | 1,0 | 0,5 | 0,2 | 0,1 | 0,05 | 0,01 | 0,005 | 0,001 |
| Гидравлическая крупность, мм/с | 0,08 | 0,03 | 0,0008 |
Взвешенные наносы. Наносы во взвешенном состоянии перемещаются вследствие турбулентного характера движения воды. Частицы наносов, имеющие относительный вес, значительно превышающий вес воды, могут находиться во взвешенном состоянии только благодаря наличию вихревых токов, направленных вверх. Подъем частиц вверх возможен при условии, что вертикальная составляющая скорости движения воды больше гидравлической крупности частиц. В турбулентном потоке на выступах дна зарождаются вихри с горизонтальной осью вращения. Они срываются и поднимаются вверх, одновременно перемещаясь по течению. Такие поднимающиеся вихреобразования могут захватить со дна частицы наносов и перемещать их толщу потока.
На участках рек с большими скоростями течения - перекатах - часть наносов, перемещавшихся до этого по дну, переходят во взвешенное состояние. На участках, где скорости уменьшаются - плесах - происходит отложение (аккумуляция) более крупных частиц. Распределение взвешенных наносов в живом сечении потока неравномерное. Более насыщены наносами нижние слои, где преобладают более крупные частицы. Движение взвешенных наносов носит пульсирующий характер, соответствующий пульсации скорости течения воды.
Количество взвешенных наносов в реке зависит от скорости течения и, главным образом, от поступления наносов с водосборного бассейна. Взвешенные наносы составляют основную часть расхода наносов рек. На равнинных реках взвешенные наносы могут составлять до 90-95% всего количества наносов.
Измерение расхода и стока взвешенных наносов.
Количество наносов, проносимых через живое сечение потока в единицу времени, называют расходом наносов. Отношение расхода взвешенных наносов (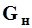 ) к расходу воды (
) к расходу воды (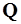 ) представляет среднюю мутности всего потока (
) представляет среднюю мутности всего потока (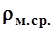 ), поэтому
), поэтому
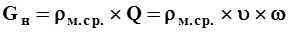 (3) (3)
| (3) |
Уравнение (3) основано на том, что частицы взвешенных наносов перемещаются с той же скоростью, что и вода. Различают местную мутность (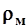 ) и среднюю мутность на вертикали (
) и среднюю мутность на вертикали (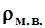 ).
).
Для учета взвешенных наносов берут пробы воды приборами, называемыми батометрами. Различают батометры мгновенного и длительного наполнения. Батометры мгновенного наполнения в сети Гидрометслужбы в настоящее время не применяются.
Батометры длительного наполнения при взятии пробы выдерживают в каждой точке в течение времени необходимого для наполнения прибора водой. Соответственно, батометры длительного наполнения в той или иной степени учитывают пульсацию мутности. В настоящее время применяют батометры длительного наполнения следующих типов: а) батометр-бутылка на штанге и в грузе; б) ваакумный батометр. В последние годы получает развитие фотометрический метод определения мутности.
Измерение расхода взвешенных наносов производится совместно с измерением расхода воды и поэтому включает в себя операции, необходимые для измерения расхода воды (измерение уровня воды и уклона водной поверхности, промеры глубины, измерение скоростей течения); дополнительно берут пробы воды на мутность.
Расходы взвешенных наносов в гидрометрических створах измеряют точечным, суммарным и интеграционным способами. Точечный способ заключается в том, что пробы воды берут в отдельных точках скоростных вертикалей; применяется в трех разновидностях: детальном, двухточечном и одноточечном. При детальном способе пробу воды берут в пяти точках на вертикали: у поверхности, на 0,2h, на 0,6h, на 0,8h и у дна. На вертикалях с малыми глубинами число точек сокращают: пробы берут в двух точках (0,2h, 0,8h) или в одной точке (0,6h).
Двухточечный способ применяют на больших и средних реках при небольшой мутности, в пределах 50-100 г/м3. Одноточечный способ применяют при такой же мутности, но на малых реках.
Суммарный способ заключается в том, что пробы воды берутся в двух точках на каждой вертикали (0,2h, 0,8h), а затем сливаются в общий сосуд и определяется мутность суммарной пробы.
Интеграционный способ заключается в том, что проба воды забирается непрерывно по всей глубине вертикали при перемещении батометра от поверхности ко дну и обратно.
Вычисление расхода взвешенных наносов. При измерениях расхода взвешенных наносов точечными способами необходимо вычислить средние единичные расходы взвешенных наносов для каждой скоростной вертикали.Единичным расходом наносов называется количество наносов в граммах проносимых на каждый м2 поперечного сечение потока за единицу времени (г/м2.с). При двухточечном способе взятия пробы единичный расход вычисляют по формуле
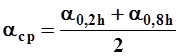 (4) (4)
| (4) |
где 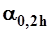 - единичный расход взвешенных наносов в точке на глубине 0,2h и
- единичный расход взвешенных наносов в точке на глубине 0,2h и 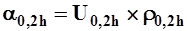 ;
; 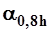 - единичный расход взвешенных наносов в точке на глубине 0,8h и
- единичный расход взвешенных наносов в точке на глубине 0,8h и 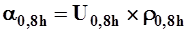 .
.
При одноточечном способе взятия проб средний единичный расход на вертикали вычисляют по формуле
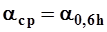 (5) (5)
| (5) |
где 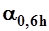 - единичный расход взвешенных наносов в точке на глубине 0,6h, равный
- единичный расход взвешенных наносов в точке на глубине 0,6h, равный 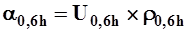 , (г/(м2с)).
, (г/(м2с)).
Если измерение расхода взвешенных наносов производилось в заросшем водной растительностью русла или при ледяном покрове и пробы брались в точках 0,15h и 0,85h рабочей глубины, то средний единичный расход наносов на вертикали вычисляется по формуле
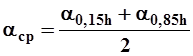 (6) (6)
| (6) |
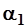
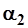

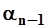
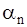













 |  | ||

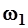
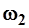
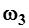
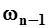
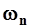
Рис.1. Схема к вычислению расхода взвешенных наносов аналитическим способом.
После того как для всех вертикалей определены средние единичные расходы взвешенных наносов, общий расход находят по формуле
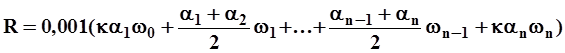
| (7) |
где 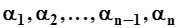 - единичные расходы взвешенных наносов на скоростных вертикалях в г/(м2с);
- единичные расходы взвешенных наносов на скоростных вертикалях в г/(м2с); 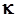 - коэффициент, зависящий от характера распределения скоростей в прибрежной зоне;
- коэффициент, зависящий от характера распределения скоростей в прибрежной зоне; 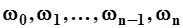 - частичные площади живого сечения, м2.
- частичные площади живого сечения, м2.
В реальных системах присутствуют диссипативные силы, которые оказывают демпфирующее воздействие на колебательную систему (например, внутренние силы вязкого трения) Но это демпфирование в большинстве случаев невелико. Оно существенно не сказывается на частотных характеристиках, однако ограничивает резонансные пики конечными значениями и несколько сглаживают фазочастотные характеристики.
Нетрудно установить, что частотные характеристики абсолютно упругой системы, приводимой к одномассовой, совпадают во всем диапазоне с частотными характеристиками идеального интегрирующего звена, а структурная схема принимает вид
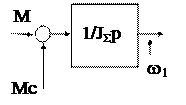 |
Механические переходные процессы
Изменение управляющего или возмущающих воздействий вызывают в механической подсистеме переходные процессы, называемые механическими переходными процессами.
Рассматривая одномассовую систему, движение которой описывается дифференциальным уравнением первого порядка
JS dw/dt= M- Mc,
где JS = J1+J2 и Mc= Mc1 + Mc2,
легко установить, что при постоянстве статического момента сопро-тивления закон изменения скорости в переходном процессе определяется характером изменения во времени управляющего момента. Так для получения экспоненциальной кривой скорости при пуске необходимо обеспечить экспоненциальную зависимость момента от времени. Для получения равномерно ускоренного изменения скорости необходимо формировать прямоугольный закон изменения момента двигателя во времени (см. рис. 6.4,а,б).
| wкон M, w w(t) M(t) Mc |
wкон
M, w
w(t)
M(t)
Mc
|
Если известен характер изменения момента двигателя и приведенного момента нагрузки с помощью указанного уравнения можно установить характер изменения скорости не прибегая к его решению. Механическая часть, представленная в виде жесткого звена, как отмечалось, отражает движение системы в среднем и не дает точного представления о характере движения упруго связанных масс. С целью выяснения этого влияния рассмотрим реакцию на скачок момента от 0 до M в двухмассовой системе при нулевых нагрузках Mc1 и Mc2 и нулевых начальных условиях.
Найдем вначале реакцию координаты w2 , используя ранее полученную передаточную функцию (6.5). Операторное изображение интересующей нас величины при M(p)= M/p равно
w2(p)= 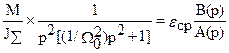 ,
,
где e ср - среднее значения ускорения второй массы, B(p)=1 и
A(p)= p2[(1/W02)p2+1]-
полином с корнями p1,2 =0 и p3,4=±jW0
Решение найдем по формуле разложения в виде суммы двух составляющих
w2(t) = w‘(t) +w“(t),
первая из которых обусловлена парой нулевых корней, а вторая- парой комплексно-сопряженных корней.
Пользуясь модификацией формулы разложения для случая n кратных корней полинома знаменателя
x(t)= 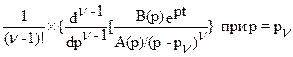
получим
w‘(t) = 
или
w‘(t) = 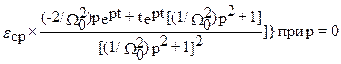
После подстановки p=0, получим
w‘(t)= e ср t.
Из курса математики известно, что пара комплексно сопряженных корней pi,i+1 определяет во временной области составляющую решения вида
x(t)= 2Re 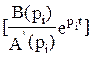
В нашем случае
A’(p)=dA(p)/dp= -2jW 0
и потому
w“(t)= e ср ´2Re  = -(e ср/W0) Sin W0t
= -(e ср/W0) Sin W0t
Таким образом получили окончательное решение
w2(t) = w‘(t) +w“(t) = e ср t -(e ср/W0) Sin W0t
График зависимости w2(t) представлен на рис.6.5.. Видно, что скорость w2 (t) в среднем меняется по линейному закону с ускорением eср=M/JS и содержит незатухающую гармоническую составляющую с амплитудой e ср/W0 и частотой W0.
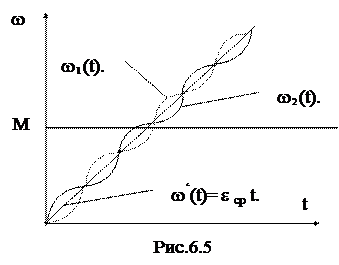
Определим теперь скорость первой массы, используя выражение для передаточной функции (6.4), которое можно представить в виде суммы
Ww1M(p)= Ww2M(p)+ 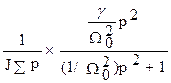 ,
,
первое слагаемое которой является передаточной функцией Ww2M(p).
Следовательно, решение w1(t) будет содержать три составляющие, две из которых w‘(t) и w“(t) нами уже найдены, а третье можно определить из выражения
w’”(t) =L-1 { 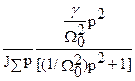 ´ M/p }
´ M/p }
или
w‘’’(t) =L-1 { 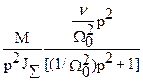 }=
}=
=(eср g/W02) L-1 { 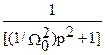
Принимая В(P)=1 и A’(p)= p(2/W02) и при p=jW0 A’(jW0)= 2j/W0, получим
w‘’’(t) =(eср g/W02) 2Re 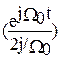 = eср g/W0 Sin W0t
= eср g/W0 Sin W0t
Эта составляющая отмечена штриховой линией на уже рассмот-ренном рисунке. Она находится в противофазе с колебаниями w’’(t) и потому колебания скорости w1(t) меньше, чем w2(t). При прочих равных условиях колебания скорости w1(t) тем меньше, чем меньше J2, а увеличение W0 при тех же ускорениях снижает амплитуды колебаний как первой, так и второй массы. Эти выводы полностью согласуются с результатами частотного анализа. Под действием сил внутреннего вязкого трения эти колебания в действительности являются затухающими во времени, однако время затухания достаточно велико.
|
|
|
|
Дата добавления: 2014-01-14; Просмотров: 688; Нарушение авторских прав?; Мы поможем в написании вашей работы!