Лекция20

NZQRC

Медленная и быстрая составляющие продольного возмущенного движения

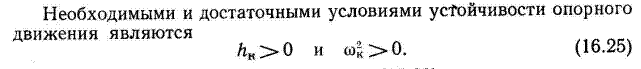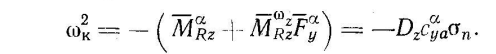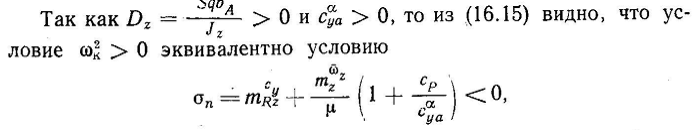16.3 Короткопериодическое возмущенное движение

16.4 Длиннопериодическое возмущенное движение

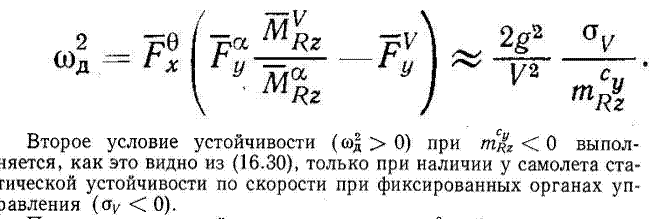
Часто используемые подмножества множества R: интервалы, отрезки, полуинтервалы, конечные, бесконечные, ε-окрестности.

Логические символы и общепринятые обозначения:

.

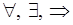Примеры.

1. Утверждение «Для любого х, взятого из отрезка [-1, 2], можно найти y на отрезке [1, 4], такое, что y = x²» записывается так

.

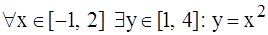Отображения множеств. Функции. Однозначность. Взаимная однозначность. Изоморфизм.

Мощность множества.

Определение. Мощностью μ(М) множества М наз. его количественная мера, обладающая след. свойствами:

1) Для конечного множества μ(М) = числу элементов в М

2) Если между А и В сущ. вз.-одн. соответствие, то μ(А) = μ(В)

3) Если сущ. вз.-одн. соответствие между А и подмножеством В, то μ(А) ≤ μ(В)

4) Если сущ. вз.-одн. соответствие между А и подмножеством В и нельзя установить вз.-одн. соответствие между А и В,

то μ(А) < μ(В)

Любое бесконечное множество содержит подмножество, которое можно пронумеровать или пост. вз.-одн. соответствие с N.

Значит, N имеет наименьшую бесконечную мощность. Множ-ва, имеющие мощность, равную мощности N, наз. счётными. Мощность счётного мн-ва обозначается 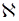₀.

Показать, μ(N) = μ(Z) = μ(Q) =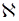₀.

Продемонстрировать нумерацию (вз. одн. соотв-е) целых чисел

N: 1 2 3 4 5 6 7 …

Z: 0 1 –1 2 -2 3 –3 …

Всякое рациональное число можно поместить в таблицу, элементы которой нумеруются начиная с угла по диагоналям. (Прокомментировать насчёт нуля, повторяемости и знаков).

						…	m	…
		±2/3
			±3/4
..
n							±m/n
..

Показать, μ(R) > 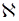₀.

Предположим противное, т.е. μ(R) = 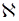₀, значит все действитель-ные числа можно пронумеровать. Рассмотрим только числа на интервале (0, 1) и предположим, что они пронумерованы:

а₁, а₂, а₃, … Запишем каждое из этих чисел в десятичной форме с неограниченным числом знаков после запятой.

а₁ = 0. α₁₁ α₁₂ α₁₃…

а₂ = 0. α₂₁ α₂₂ α₂₃…

а₃ = 0. α₁₃ α₃₂ α₃₃…

……………………

Рассмотрим число а = 0. α₁ α₂ α₃… такое, что

α₁ ≠ α₁₁, α₂ ≠ α₂₂, α₃ ≠ α₃₃,…

Тогда a ≠ a₁, a ≠ a₂, a ≠ a₃,…, а значит, числа а нет в списке. Получилось противоречие.

Рассмотреть множество всех подмножеств конечного множества.

Вывести формулу.

Терема Кантора. Мощность любого непустого множества всегда меньше мощности множества всех его подмножеств.

Доказательство от противного.

Пусть имеется взаимно-однозначное соответствие f между элементами множества М и его подмножествами:

x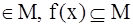. Тогда М можно разбить в объединение двух непересекающихся подмножеств: М = A U B,

А состоит из таких элементов х, для которых x,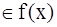

B состоит из таких элементов х, для которых x.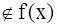

Тогда найдётся такой элемент b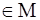, что B = f(b).

Рассмотрим, в каком из подмножеств A или В находится элемент b.

1) Допустим, что b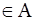. Тогда, по определению A, 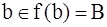, что невозможно, так как А∩В = Ø.

2) Допустим, что b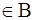. Тогда, по определению В, 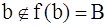, что невозможно.

Получилось противоречие. Теорема доказана.

Дать определения континуума и гиперконтинуума 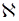₁ и 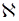₂. Рассказать о континуум-гипотезе.

Теорема. μ(R) = 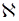₁.

Док-во. Рассмотрим множество действительных чисел в интер-вале (0, 1). Такие числа в двоичной форме имеют однозначную запись в виде 0. α₁ α₂ α₃…, где α₁, α₂, α₃ … - либо 1, либо 0. Рассмотрим такое число:

а = 0. 1 0 1 1 0 0 0 1 0 1 …

N = { 1 2 3 4 5 6 7 8 9 10 … }

f(a) = { 1 3 4 8 10 … } .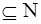

Видим, что имеется взаимно-однозначное соответствие f между действительными числами а из интервала (0, 1) и подмножествами f(a) множества натуральных чисел, ч.т.д.

Теперь установим взаимно-однозначное соответствие между интервалом (0, 1) и всей числовой осью. Согнём интервал (0, 1) в полуокружность и расположим над числовой осью, как показано на рисунке:

R

Отметить, что мощность гиперконтинуума имеет множество всех функций на отрезке.

Дата добавления: 2014-01-14