Метод бисекции

Итерационное уточнение корней

Перейдём ко второму этапу решения поставленной задачи.

Итерационное уточнение корней – это вычислительный метод уточнения корня с заданной точностью.

Рассмотрим некоторые из этих методов.

Также называется метод деления отрезка пополам. Это простейший и достаточно надёжный метод итерационного уточнения корней.

Пусть 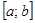– отрезок, являющийся результатом локализации, при этом функция на нём непрерывна и 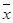– единственный корень на данном интервале.

Важное примечание. С помощью записи 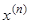будем обозначать приближение корня 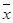, найденного на итерации с номером .

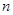Шаг1: Задаём 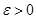– точность вычисления результата. Покажем , , ,

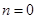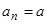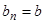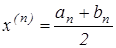
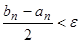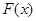Шаг 2: Если , то , иначе переход к шагу 3.

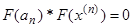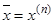Шаг 3: Если , то , иначе переход к шагу 4.

Шаг 4: Если 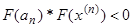, то полагаем 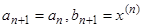и переход к шагу 6, иначе переход к шагу 5.

Шаг 5: Полагаем

Шаг 6: Полагаем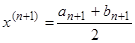

Шаг 7: , переход к шагу 2.

Примечания

1. Критерием останова алгоритма является достижение заданной точности. Тем не менее, для предотвращения отказа машины от облуживания в более сложных случаях необходимо также предусмотреть ограничение по количеству итераций.

2. Этот алгоритм неприменим для нахождения корня кратной чётности, т.к. .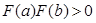

3. Замечание относительно погрешности. Если корень 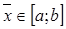, то погрешность приближения не превышает половины длины отрезка :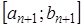

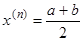
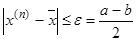
Задача 1.4.

Рассмотрим уравнение

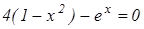
Найти методом бисекции с точностью 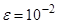положительный корень уравнения .

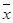В предыдущем примере этот корень 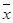был локализован на.

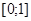Примем

Положим ; ;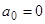

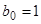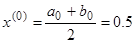
Результаты нескольких итераций приведены в таблице:

Ит.	Значения	Точность	Что дальше
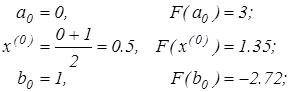
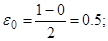
			Знак меняется в правой части, убираем левую
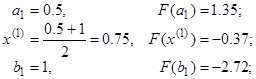
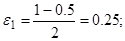
			Знак меняется в левой части, убираем правую
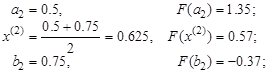
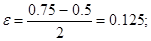
			Убираем левую часть
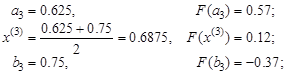
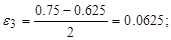
			Убираем левую часть
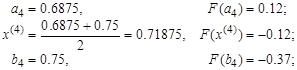
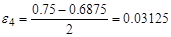
			Убираем правую часть
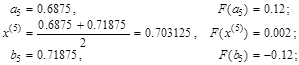
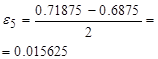
			Убираем левую часть
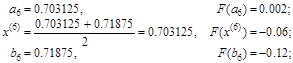
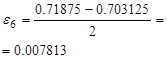
			Достигнута заданная точность

Ответ: При имеем 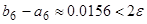. Заданная точность 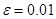достигнута. Можно принять .

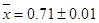Дата добавления: 2014-01-15