Метод простой итерации

Преобразуем исходное уравнение 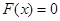к следующему эквивалентному виду:

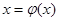
Далее выбираем каким-либо образом начальное приближение 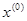и подставляем его в правую часть нового уравнения. То что получилось в результате этой подстановки, обозначим :

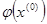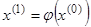
Получаем новое приближение 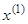. Снова подставляем его в правую часть, новое приближение также подставляем и т.д.

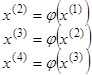
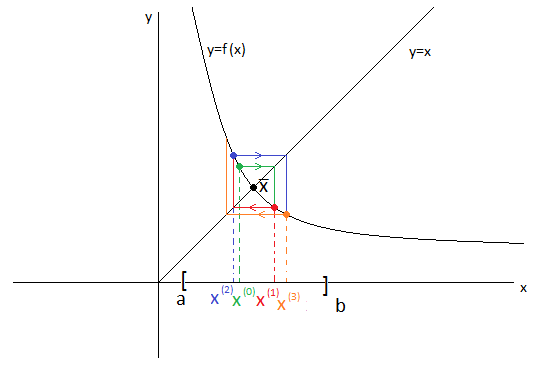
Таким образом мы организуем следующий итерационный процесс

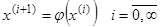
Если 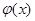- непрерывная функция, а последовательность 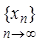сходится, то существует предел, являющийся решением этого уравнения:

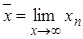
Обоснование.

Пусть выражение 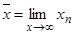верно.

Тогда перейдём к пределу в равенстве, описывающем итерационный процесс. Получаем:

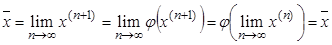
Так как 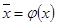, то и .

Примечание. Возможны ситуации, когда последовательность 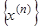при 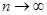является расходящейся. В таких ситуациях метод простой итерации применять нельзя.

Достаточное условие сходимости итерационного процесса (4) формулируется в виде следующей теоремы:

Теорема.

Пусть уравнение 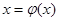имеет единственный корень 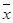на интервале 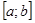. Тогда итерационная последовательность сходится для 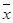при 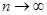для любых 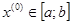, если выполнены следующие условия:

1. Функция 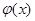определена и дифференцируема на этом интервале

2. Её производная такова, что 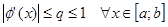(скорость роста функции по модулю меньше чем единица)

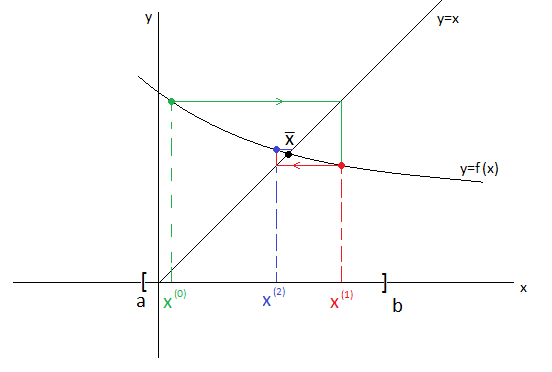
Вот геометрическая интерпретация достаточного условия сходимости.

Случай А. Производная функции положительна на отрезке 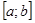и везде по модулю меньше единицы (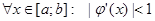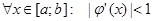). Это означает что угол наклона касательной в каждой точке исходной функции больше 45° (), то есть наша функция монотонно убывает и является вогнутой и угол наклона её касательных изменяется от 0° до 45°.

Тогда последовательность сходится колебательно.

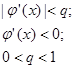
Случай В. Производная функции положительна на отрезке 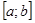и в некоторых местах становится больше единицы (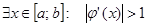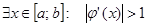). Это означает что в функции найдутся места, в которых угол наклона касательной меньше 45°.

Тогда последовательность расходится, потому что не выполняется достаточное условие. Причём расходимость колебательная.

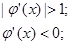
Оценка погрешности.

Критерий окончания итерационного процесса определяется на основе априорной оценки процесса.

Пусть выполнено достаточное условие сходимости. Тогда верна следующая апостериорная оценка погрешности:

,

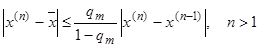Где 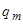- максимальная скорость роста производной.

Из этой формулы следует, что вычисления стоит вести до выполнения следующего условия:

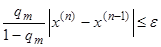
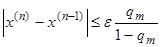
Процесс должен быть остановлен после достижения заданной точности.

Задача 1.5.

Решить уравнение 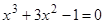методом простой итерации с точностью 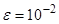. Найти корень на интервале .

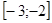Решение. Так как на заданном интервале 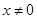, то преобразование к виду 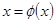можно выполнить делением обеих частей на :

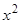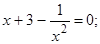
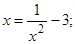
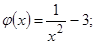
Проверим достаточное условие сходимости:

1. Производная 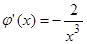на отрезке 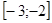существует

2. - скорость роста функции по модулю меньше 1

Вычислим критерий останова:

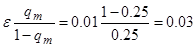
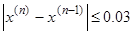
Пусть начальным приближением будет середина заданного отрезка 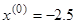. Тогда мы можем начать итерационный процесс:

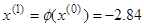
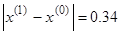
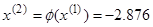
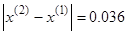
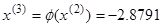
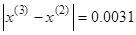
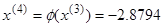
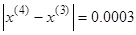	- условие останова выполнено

Ответ:

Дата добавления: 2014-01-15