Метод Ньютона-Рафсона

Предположим, что уравнение 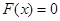имеет единственный корень 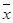на отрезке 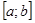, и производнаяна этом отрезке существует, непрерывна и отлична от нуля.

Тогда разложим функцию в ряд Тейлора (т.е. осуществим линеаризацию):

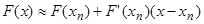
Причём точность приближения увеличивается при .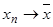

Дальше вместо исходного уравнения мы будем решать это приближённое уравнение:

Разрешив его относительно , получим:

Основная формула метода Ньютона-Рафсона имеет вид:

Метод Ньютона-Рафсона хорош тем, что использует более точные знания о поведении функции и поэтому сходится гораздо быстрее, чем метод простой итерации.

Формула Ньютона-Рафсона и сам метод имеет следующую геометрическую интерпретацию:

1. В точке график 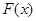заменяется на касательную.

2. Точка пересечения касательной с осью 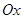принимается за новое приближение .

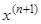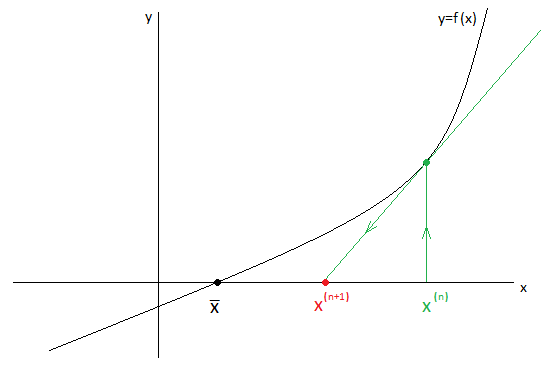
3. Далее строится точка 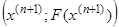, в которой снова строится касательная.

4. И так далее до тех пор, пока не будет достигнута заданная точность.

Обоснование.

Будем обозначать отрезок как .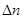

Тогда тангенс угла наклона, или производная в точке касания будет равна 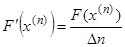, значит . С учётом формулы Ньютона-Рафсона: .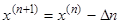

Примечание 1.

Формулу Ньютона-Рафсона можно интерпретировать следующим образом.

Предположим, что . Тогда перейдём от уравнения 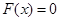к равносильному уравнению , и на основании формулы Ньютона-Рафсона это будет означать, что:

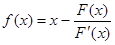
Применительно к уравнению вида 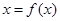метод Ньютона-Рафсона реализует схему метода простых итераций. При этом:

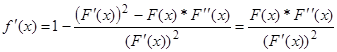
Тогда по определению следует, что

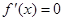
Примечание 2.

Насчёт скорости сходимости. Если точку выбрать достаточно близкую к 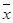, то скорость убывания погрешности 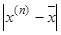здесь выше, чем в методе простой итерации. Там скорость сходимости линейная, здесь – квадратичная.

Примечание 3.

Есть и такие случаи, когда очень близкое приближение может привести к бесконечному циклу – бывают и такие крайне выпуклые функции.

Дата добавления: 2014-01-15