Закони розподілу дискретних випадкових величин

V. Підведення підсумків заняття

ІV. Узагальнення та систематизація знань

План

ІІІ. Виклад нового матеріалу

І. Організаційний момент

Хід заняття

Лекція 13

Домашнє завдання.

1)Підручник:

2) опорний конспект,

3) підготувати реферати: Харківщина у роки Великої Вітчизняної війни; Медики Харкова у роки війни; Націоналістичний рух опору на Харківщині.

Тема: Закони розподілу випадкових величин

Мета: Ознайомити студентів з основними законами розподілу випадкових величин.

Література

1. Соколенко О. І. Вища математика. Підручник. К.: Академія, 2002.

2. Литвін І.І. та інш. Вища математика. Навчальний курс. Л.: Глобус, 2002.

3. Овчинников П.П. Вища математика. Ч.2. – К.: Техніка, 2004.

а) готовність групи до заняття;

б) перевірка присутніх.

ІІ. Актуалізація опорних знань студентів

а) повідомлення теми та мети заняття;

б) відповіді на запитання раніше вивчених лекцій.

1. Закони розподілу дискретних випадкових величин

1.1. Біноміальний розподіл

1.2. Пуасонівський закон розподілу

1.3. Геометричний закон розподілу

2. Закони розподілу неперервної випадкової величини

2.1. Рівномірний закон розподілу задається густиною розподілу

2.2. Показниковий (експоненціальний) розподіл.

VІ. Домашнє завдання: вивчити матеріал лекції.

Зміст лекції

Задають дискретні випадкові величини за допомогою закону розподілу, коли задаються ймовірності їх можливих випадкових значень. Залежно від того, за якою формулою будуть обчислюватися ймовірності Р_і, ці закони будуть мати свою назву.

1.1. Біноміальний розподіл – це закон розподілу випадкових величин, заданий таблицею, у якій ймовірності Р_і обчислюються за формулою Бернуллі:

.

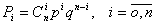Х	0	1	…	і	…	n
р	q^n	C^1np q^n-1	…	C^1np^i q^n-1	…	p^n

де p, n, q = 1-p, називаються араметрами розподілу.

Математичне сподівання і дисперсія випадкової величини, що має біноміальний розподіл відповідно рівні:

.

Приклад 1. Митний пост дає статистичну оцінку того, що 20% усіх осіб, що повертаються з-за кордону, не декларують весь товар, який підлягає оподаткуванню. Якщо випадково відібрати 5 осіб, то записати закон розподілу випадкової величини Х – кількість осіб, що не декларують весь товар, привезений з-за кордону та знайти математичне сподівання і середнє квадратичне відхилення.

Рішення. В даному випадку р=0,2; q=0,8; n=5.

Тоді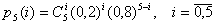

Х
Р	0,32768	0,4096	0,2048	0,0512	0,0064	0,0032

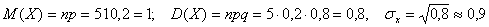
1.2. Пуасонівський закон розподілу – це закон розподілу випадкової величини, заданий таблицею, у якій ймовірність обчислюється за формулою Пуассона .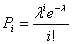

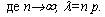
Типовими прикладами випадкової величини, що має розподіл Пуассона, є: число викликів на АТС за деякий час t; число відновлень складної апаратури за час t, якщо відомо, що відновлення незалежні один від одного і в середньому на одиницю часу випадає l відновлень і т.п.

Розподіл Пуассона залежить від одного параметру l, який є математичним сподіванням випадкової величини Х:

.

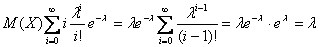Дисперсія буде:

звідси: .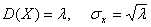

Приклад 2. Завод відправив споживачу 5000 якісних виробів. Ймовірність пошкодження виробу в дорозі рівна 0,0002. Записати закон розподілу чотирьох пошкоджених виробів та зобразити його графічно.

Рішення. З умови: l=np=5000× 0,0002=1 тому

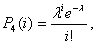P₄(0)=0,36788,

P₄(1)=0,36788, P₄(2)=0,0,18394, P₄(3)=0,06131, P₄(4)=0,01533.

Х
Р	0,36788	0,36788	0,18394	0,06131	0,01533

Дата добавления: 2014-01-15