Рівномірний закон розподілу задається густиною розподілу

Закони розподілу неперервної випадкової величини

При розв’язанні практичних задач, приходиться зустрічатись з різними розподілами неперервних випадкових величин. Густини розподілу неперервних випадкових величин також називаються законами розподілу.

,

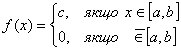де С = const.

Тому запишемо

,

Знайдемо інтегральну функцію розподілу F(x), яка буде:

.

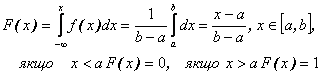Тобто ,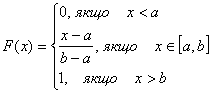

а її графік буде

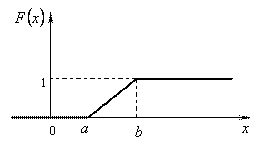
Знайдемо числові характеристики розподілу:

а) математичне сподівання:

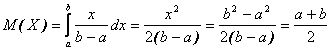
б) дисперсія: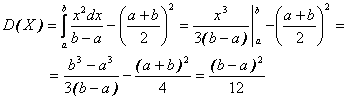

в) середнє квадратичне відхилення: .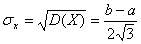

2.2. Показниковий (експоненціальний) розподіл, коли випадкова величина має густину розподілу у вигляді:

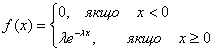
де l - параметр розподілу.

Випадкова величина Х з таким законом розподілу часто зустрічається в прикладних питаннях теорії ймовірності, особливо в теорії масового обслуговування.

Знайдемо інтегральну функцію розподілу:

,

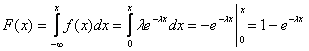тобто .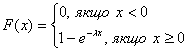

Наведемо графіки функцій 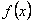і :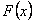

Знайдемо числові характеристики показникового розподілу:

а) математичне сподівання;

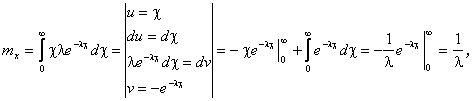тобто ;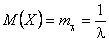

б) дисперсія:

в) середнє квадратичне відхилення: .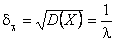

Отже, .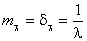

Приклад 1. Випадкова величина Т – час роботи елементу – має показниковий розподіл. Знайти ймовірність того, що час роботи елементу буде не менше 600 годин, якщо середній час роботи елементу 400 годин.

Рішення. За умовою математичне сподівання (середній час роботи елементу) , значить:

.

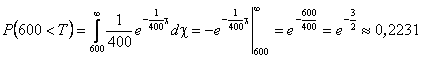Дата добавления: 2014-01-15