Условия применения

Вообще говоря, системы с нечеткой логикой целесообразно применить для сложных процессов, когда нет простой математической модели; если экспертные знания об объекте или о процессе можно сформулировать только в лингвистической форме.

Данные системы применять нецелесообразно, когда требуемый результат может быть получен каким-либо другим (стандартным) путем, или когда для объекта или процесса уже найдена адекватная и легко исследуемая математическая модель.

Отметим, что основные недостатки систем с нечеткой логикой связаны с тем, что:

– исходный набор постулируемых нечетких правил формулируется экспертом-человеком и может оказаться неполным или противоречивым;

– вид и параметры функций принадлежности, описывают их входные и выходные переменные системы, выбираются субъективно и могут оказаться не вполне отражающими реальную действительность.

Приближенные рассуждения в прикладных задачах

Проиллюстрируем применение аппарата приближенных рассуждений на примере нечетких контроллеров. Под нечеткими контроллерами понимается программно-аппаратные системы, управляющие некоторыми процессами (от английского слова control - управление). Такого рода системы имеют огромное число приложений - от бытовой техники до управления сложными технологическими процессами. Рынок нечетких контроллеров оценивается в миллиарды долларов.

Для описания нечетких управляющих систем сформулируем основные понятия теории управляющих систем в классическом понимании.

Система управления на основе наблюдений среды и объекта управления и соответствия этих наблюдений цели формирует решение по выбору управляющего воздействия на объект (в частном случае это может быть "пустое" решение).

Если при сложившейся ситуации в среде и на объекте управления цель достигнута - продолжается наблюдение за средой и объектом.

Если цель не достигается - необходимо некоторое воздействие на объект. Это воздействие выбирается блоком принятия решений на основе модели среды и модели объекта управления и выполняется блоком реализации решений.

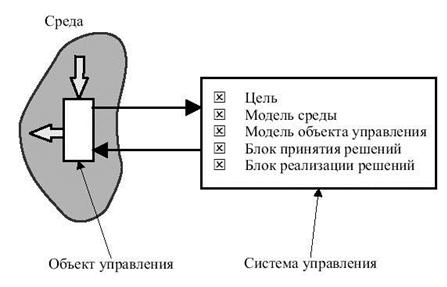
Воздействие вызывает переход объекта в новое состояние и, как следствие, некоторые возмущения в среде. Новое состояние пары "объект управления - среда" может быть ближе к цели или, наоборот, удалять нас от нее.

Мы можем оценить это, наблюдая объект и среду и сравнивая сложившуюся реальную ситуацию с целью.

Результат такого наблюдения и сравнения инициирует либо новые решения в случае, когда цель не достигается, либо пассивное наблюдение в случае, когда цель достигнута.

Как видно из приведенного краткого обзора основных понятий теории управления, применение классических методов возможно при наличии модели среды и модели объекта управления.

Что делать, если таких моделей нет? Или модели есть, но для их "обсчета" требуются значительные ресурсы?

Для "модельных" задач последнее может быть не существенным, однако для практических задач большие ресурсы могут быть критичными (например, для систем управления в реальном времени управляющее воздействие должно вырабатываться не более, чем за некоторое время Δt, иначе решение, пусть самое лучшее, уже никому не нужно; для бортовых систем управления критичным могут быть габариты и вес компьютера: если для работы с моделью требуется супер-ЭВМ, то ее не возьмешь в самолет или автомобиль).

При фиксированной цели управления (например, сохранение значения управляемого параметра g в некоторой области допустимых значений G) модель процесса управления может быть выражена в виде множества "Если …, то …" - правил следующим образом.

Пусть состояние управляемого объекта G описывается набором значений качественных признаков I(Θ). Множество значений признаков D фиксировано и является конечным (D = {d1, …, dm}). Процесс описывается последовательностью состояний объекта в моменты времени t1, t2, … .

Для достижения цели управления ("удержания" значения управляемого параметра g в области G в нашем случае) у нас есть возможность изменять значения некоторых управляемых параметров из множества A = {a1, …,an}.

Для описания идеи использования нечетких лингвистических регуляторов рассмотрим простейшую ситуацию m = 1, n = 1, то есть ситуацию, когда D = {d}, A = {а}.

Как отмечалось выше, эксперт часто может сформулировать свой опыт управления только для качественных значений d и а. Пусть d = {d1, …, ds} и а = {а1, …, аr} - набор качественных значений d и а соответственно. Моделью d и а может служить лингвистическая переменная с фиксированным множеством значений или, что то же самое - семантическое пространство. В этом случае d и а - названия соответствующих лингвистических переменных, di и аj (i = 1, …, s; j = 1, …, r) - ее значения.

Пример

Пусть соответствующие нечеткие множества 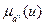и определены в универсальных множествах U и V соответственно (i = 1, …, s; j = 1, …, r). Тогда правила, которые использует эксперт, можно сформулировать следующим образом: "Если d = di то а = аj". Например, "Если давление пара очень высокое, то открыть клапан сильно".

Дата добавления: 2014-01-15