Показатели центральной тенденции

Ряды распределения численностей показывают, что варианты концентрируются около некоторого центрального их значения. Следовательно, можно найти такое значение варианты или абстрактное среднее число, которое будет наиболее представительной характеристикой данной совокупности.

Ряд показателей центральной тенденции включает:

· среднюю арифметическую;

· среднюю квадратическую;

· среднюю геометрическую;

· среднюю гармоническую;

· моду;

· медиану.

Назначение средних величин состоит в том, чтобы отразить какое-нибудь одно свойство совокупности, например, среднюю длину, среднюю массу, средний объем.

То свойство (или тот признак) совокупности, которое остается неизменным при замене отдельных значений их средним значением, называется определяющим свойством.

Средняя отражает определяющее свойство так, что образуемая с ее помощью абстрактная совокупность равных ей чисел по величине определяющего свойства не отличался от реальной.

Средняя арифметическая. Средняя арифметическая - наиболее часто употребляемый статистический показатель центральной тенденции. Она является центром тяжести распределения.

Среднюю арифметическую генеральной совокупности обычно обозначают m, а среднюю арифметическую выборочных наблюдений - М (или ). Она имеет ту же размерность, что и варианты.

Средняя арифметическая получается путем деления суммы всех вариант (x₁, x₂,..., x_n) на объём выборки:

M = (x₁+ x₂ +... + x_n)/N= (Sx)/N, (1)

где

N - общее число вариант;

S - знак суммирования.

Группируя варианты по их величине, получим следующий ряд:

x
n

M= (1*15+3*20+ 1*25)/5 = 20 см.

Средняя геометрическая. При рассмотрении среднего темпа роста изучаемого признака средняя арифметическая не пригодна. Вместо нее вычисляют среднюю геометрическую Mg (или g) по формуле:

Mg = 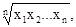(2)

где

x₁, x₂,..., x_n - темпы роста (величины, показывающие, во сколько раз увеличивался признак от периода к периоду);

n -число периодов.

При n >2 формулу удобнее применять в логарифмическом виде:

lgMg = (lgx₁+ lgx₂ +... + lgx_n)/n. (3)

Если данные, для которых вычисляют среднюю геометрическую, должны быть взвешены, то формула имеет вид:

lgMg = (n₁lgx₁+n₂ lgx₂ +... +n_n lgx_n)/N. (4)

Исходя из содержания формул среднюю геометрическую называют также средней логарифмической, так как ее логарифм есть арифметическая средняя логарифмов составляющих величин.

Средняя квадратическая. В лесном хозяйстве нередко приходится находить сумму площадей сечений деревьев в древостое располагая распределением числа деревьев по ступеням толщины.

Так, для ряда распределения 94 деревьев по ступеням толщины:

X
N
Sn

получена сумма площадей сечений всех деревьев равная 69586 см². Средний арифметический диаметр по формуле (2.2) равен 30,08 см. Площадь сечения g дерева, соответствующая этому диаметру, равна 710,7 см², а площадь сечений 94 деревьев, найденная как про­изведение gN=G, составляет 66806 см². Она на 4% меньше истинной площади сечений.

Такое же расхождение наблюдалось бы и в объеме деревьев. Определяющее свойство - площадь сечения всех деревьев древостоя выражается формулой:

G = (p/4) (n₁d₁² + n₂d₂² +…+ n_nd_n²), (5)

где

p =3,14;

n₁ n₂,..., n_n - количество деревьев в ступенях толщины;

d₁, d₂,..., d_n - диаметры ступени толщины, см.

Очевидно, что величина G пропорциональна не диаметрам, а их квадратам.

Поэтому истинная площадь сечений может быть получена через число деревьев и величину среднего квадратического диаметра.

Mq =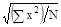 (6)

или

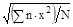Mq =, (7)

где

x² - квадраты диаметров;

n - численности деревьев в классах или группах;

N - общее число деревьев в выборке.

Найденный по формуле (7) среднеквадратический диаметр равен Mg =30,7 см. Площадь сечения, соответствующая этому диаметру, равна 740,3 см², а сумма площадей сечений 94 таких деревьев, равна 69586 см².

Таким образом, для получения истинного значения площади сечений или объемов всех деревьев посредством среднего дерева и числа деревьев диаметр дерева - модели следует находить как среднюю квадратическую величину. В лесной таксации его находят через среднюю арифметическую площадь сечения, что то же самое.

Средняя гармоническая. Для вычисления средней характеристики признаков, которые представляют собой отношение двух других варьирующих величин, пользуются средней гармонической. Среднюю гармоническую определяют по формуле:

Mh = N/(S1/x), (8)

или

Mh = N/(Sn/x), (9)

где

n - веса отдельных значений.

Так, например, при проведении рубок главного пользования пять лесозаготовительных бригад в одинаковых условиях заготовили за рабочую смену следующие количество древесины (кбм):

1-150, 2-180, 3-130, 4-200, 5-160.

Средняя производительность труда в смену составляет:

Mh = 5/(1/150+1/180+1/130+1/200+1/160) = 160,4.

Мода и медиана. Модой (Мо) называют наиболее часто встречающуюся варианту. В нормально распределенных совокупностях мода численно равна средней арифметической.

В положительно асимметричных рядах Мо > М, а в отрицательно асимметричных Мо < М.

В ряду:

X
n

Mo =28 см.

Медианой (Mе) называют значение признака, занимающее срединное положение в ряду и делящее все распределение на две равные по численности части.

Среди значений 5; 6; 7; 8; 9 Mе = 7.

Для вариационного ряда

Me = x₀ + k [ (S₁-S₂) / n ], (10)

где

x₀ - значение нижней границы класса, в котором содержится половина накопленных частот;

k - интервал;

S₁ - полусумма общей численности ряда, S₁ =N/2;

S₂ - накопленная частота, предшествующая группе, в которой находится медиана.

Для ряда распределения 94 деревьев по ступеням толщины Ме = 30

X
n
Sn

Me = 26 + 4 [(47 - 19)/28] = 30 см.

Дата добавления: 2014-01-15