Показатели вариации

Средняя величина не дает достаточного представления о свойствах изучаемой совокупности. Являясь показателем центральной тенденции, т. е. наиболее представительной характеристикой изучаемого объекта, она не характеризует степени разнообразия (изменчивости, варьирования) составляющих его единиц. Действительно, ряды из вариант 1, 3, 4, 5, 7 и 3, 4, 4, 4, 5 характеризуются одинаковой средней арифметической х =4, но отличаются по степени вариации значений признака.

Определение меры изменчивости признака или качества рассматриваемого объекта или явления считается не менее важной задачей, чем характеристика средних величин. Более того, доверие к средней величине может быть определено лишь постольку, поскольку дана оценка варьированию величин в рассматриваемой совокупности вариант.

Главной целью статистических методов является выявление вариации, которая характеризуется рядом показателей:

· размах варьирования;

· дисперсия;

· среднее квадратическое отклонение;

· коэффициент вариации;

· коэффициент дифференциации.

Размах варьирования. Разность между наибольшим и наименьшим значением признака называется размахом, который является грубым показателем варьирования признака. Однако, опираясь лишь на два крайних члена ряда, величина размаха не учитывает внутреннего, между этими крайними значениями, рассеяния вариант. Кроме того, крайние значения как редко встречающиеся члены ряда весьма неустойчивы по своему размеру и сильно зависят от объема выборочных наблюдений. Несмотря на это, при малых выборках, повторяемых несколько раз, размах варьирования нашел широкое применение.

Среднее квадратическое отклонение и дисперсия. Основным показателем вариации (изменчивости) считается среднее квадратическое отклонение, которое определяется как корень квадратный из средней арифметической квадратов отклонений вариант от их средней арифметической величины.

Среднее квадратическое отклонение для выборки обозначают через s, а для генеральной совокупности -s. Согласно определению:

s == , (11)

В математической статистике оперируют средним квадратом отклонений (s² для выборки и s² для генеральной совокупности), называемым дисперсией, которая рассчитывается по формуле (12).

s² == (12)

Для расчетов по вариационному ряду среднее квадратическое отклонение выражается формулой:

s ==

=, (13)

а дисперсия

s² ==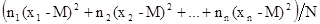

= (14)

В уравнениях (11-14)

x₁, x₂,..., x_n - варианты ряда (средние значения в классах);

M - средняя арифметическая;

n₁, n₂,..., n_n - частоты в классах;

N - общий объем ряда.

Оценивая величину s по выборочному значению s, при обработке выборки с числом наблюдений N меньше 100 в качестве делителя в формулах (11) - (14) принимают не N, а N -1. Это число называют числом степеней свободы. Такое название объясняется тем, что в статистике при вычислении любых средних величин используют число независимых величин. При вычислении s одно из отклонений оказывается несвободным. Оно равно сумме всех остальных, взятых с обратным знаком.

Таким образом, общей формулой для нахождения среднего квадратического отклонения будет:

s == , (15)

а для дисперсии

s² == (16)

При обработке вариационных рядов формулы принимают вид:

s ==

=, (17)

s² ==

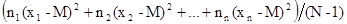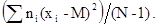= (18)

Среднее квадратическое отклонение называется также стандартным отклонением. Полученная величина является именованной и выражается в тех же единицах измерения, что и отдельные значения признака.

Средняя величина M и среднее квадратическое отклонение s дают полную количественную характеристику любой эмпирической совокупности, подчиняющейся законам распределения случайной величины.

Коэффициент вариации. Коэффициент вариации, как и s или s, является показателем изменчивости признака, выражая ее в относительных единицах. Он представляет собой среднее квадратическое отклонение отдельных вариант ряда от средней ве­личины, выраженное в процентах:

v = (s / M) 100%. (19)

Являясь показателем, не зависящим от принятых единиц изме­рения вариант, коэффициент вариации может применяться для сравнительной оценки величины варьирования различных при­знаков. Вместе с тем он в значительной степени зависит от величины средней арифметической, и поэтому его применение должно быть ограничено случаями, когда имеет место естественное от нуля начало отсчета или когда ряды распределения имеют сходные начала отсчета.

Коэффициент дифференциации. Устранить указанное ограничение позволяет коэффициент дифференциации, который без группировки вариант в классы рассчитывается по формуле:

. (20)

Для совокупностей со сгруппированными вариантами формула принимает вид:

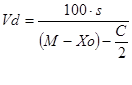, (21)

где: Xo – значение первого класса ряда распределения;

С – ширина классового промежутка.

При начале ряда распределения в пересечении осей координат, величины коэффициентов вариации и дифференциации совпадают.

Поскольку в лесоводственных и таксационных исследованияхдля нормальной кривой распределения применяется вероятность 0,99865 (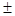3 s), то на ее основе разработана классификация степени дифференциации:

Величина коэффициента Степень дифференциации

дифференцаации

до 13% слабая

14 - 27% умеренная

28 –38%средняя (нормальная)

39- 53% значительная

54-70% большая

более 70% очень большая

Дата добавления: 2014-01-15