
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Семейство кривых распределения Джонсона
|
|
|
|
Это семейство включает три типа кривых, представляющих распределение неограниченных случайных величин (тип SU), ограниченных с одной стороны (SL) и ограниченных с двух сторон (SB).
В общем виде семейство кривых Джонсона требует знания параметра положения x, параметра масштаба l и двух параметров формы - g и d.
Тип SL. Кривая распределения ограничена слева точкой x, а значения x ³x. Этот тип распределения зависит только от трех параметров d, x и g*. Плотность распределения для нормированных значений величины x путем замены y =(x -x)/l имеет следующий вид (y ³0):
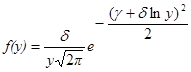 (1)
(1)
В практике использования типа SL может встретиться два случая:
величина x известна;
величина x неизвестна.
В большинстве задач по аппроксимации кривых распределения величина x, как правило, может быть определена нижней границей первого класса ряда распределения.
Если значение x неизвестно, то из формулы преобразования исходного распределения с плотностью f (x) к нормированной нормально распределенной величине z имеем:
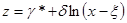 . (2)
. (2)
Так как по выборке необходимо оценить параметры g*, d и x. Для чего составляют три уравнения, приравнивающих три выборочных квантиля трем соответствующим квантилям нормированной нормально распределенной величины z
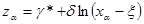 , (3)
, (3)
где z a и x a - соответственно теоретические и выборочные квантили.
Целесообразно выбирать два симметричных квантиля, что упрощает расчеты, в противном случае приходится решать нелинейное уравнение. Вполне приемлемо брать a=0,05; 0,5 и 0,95 (выбор других близких квантилей мало меняет результаты). Так как для нормированного нормального распределения |z0,05| = |z0,95| = 1.64, z0,5= 0, решением системы трех уравнений (4) находят:
 , (4)
, (4)
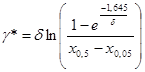 , (5)
, (5)
 . (6)
. (6)
Рассмотрим технику вычисления выравнивающих частот по уравнению типа SL на примере аппроксимации при неизвестном x.
| Х(i) | xi=c/2+xi | ni | Накоп- ленная частота | Накоп- ленная частота, % | Z | F(zi) | sum(n i) | n i | Эмпирии- ческая частота (n) | Теорети- ческая частота (n) | (n- n)2/ n |
| 2,8 | -1,86 | 0,03 | 12,38 | 12,38 | 12,4 | 0,15 | |||||
| 10,4 | -1,25 | 0,11 | 41,91 | 29,53 | 29,5 | 0,01 | |||||
| 24,4 | -0,67 | 0,25 | 98,46 | 56,55 | 56,5 | 0,04 | |||||
| 44,4 | -0,14 | 0,44 | 174,92 | 76,47 | 76,5 | 0,08 | |||||
| 64,2 | 0,36 | 0,64 | 252,42 | 77,50 | 77,5 | 0,00 | |||||
| 78,7 | 0,83 | 0,80 | 314,18 | 61,76 | 61,8 | 0,37 | |||||
| 89,1 | 1,28 | 0,90 | 354,41 | 40,23 | 40,2 | 0,01 | |||||
| 95,7 | 1,70 | 0,96 | 376,52 | 22,11 | 22,1 | 0,69 | |||||
| 98,5 | 2,10 | 0,98 | 387,04 | 10,52 | 10,5 | 0,02 | |||||
| N = 394 | 2,49 | 0,99 | 391,47 | 4,43 | 4,4 | 0,56 | |||||
| Рассчитанное значение Х2-Пирсона | 1,94 | ||||||||||
| Табличное значение Х2-Пирсона | 2,17 |
В столбец 1 таблицы 1 вписываем середины классовых промежутков Х. Во 2-ом столбце вычисляем верхние границы классовых промежутков. В 3-ем столбце вписаны частоты ряда распределения, в 4-ом рассчитывается их накопление. 5-ый столбец также содержит накопление частот, выраженное в процентах от общего числа N.
По данным столбцов 2 и 5 строим огиву ряда распределения, с которой снимаем значения квантилей, соответствующие вероятностям a, равным 0,05, 0,5 и 0,95. Они соответственно составляют 7,4; 19,1 и 33,4. При использовании этих данных по формулам (4)-(6) рассчитываются параметры ряда распределения d, g* и x:
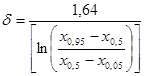 ;
;
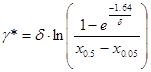 ;
;

 ;
;
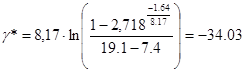 ;
;
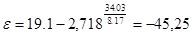
Прежде чем приступить к вычислению теоретических частот по вычисленным выборочным оценкам, по формуле (2) [ z= g*+ d×ln(xp-x) ] определяют нормированные нормально распределенные случайные величины (zi) и записывают их в столбец 6. По таблицам F (z) или непосредственно в пакете прикладных программ (в MS Excel с помощью функции F(zi) = НОРМСТРАСП (zi)) находим накопленную вероятность, соответствующую верхним границам классов ряда распределения и заносят данные в столбец 7.
В столбце 8, путем умножения величин столбца 7 на общее количество наблюдений (N), находят теоретические накопленные частоты ряда распределения. В 9-ом столбце производится вычисление частот по классам.
Правильность расчета теоретических частот ряда проверяют по величине χ2-Пирсона как сумму величин (n- n)2/ n (столбец 12). В случае (χ2р) < (χ205) Нулевая гипотеза (Н0) - принимается, т.е. различие между эмпирическим и теоретическим распределениями не достоверно.
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 1066; Нарушение авторских прав?; Мы поможем в написании вашей работы!