
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Функциональная полнота
|
|
|
|
Замкнутые классы
Пусть  множество булевых функций от n переменных.
множество булевых функций от n переменных.
Замыканием F ([F]) называется множество всех булевых функций, реализуемых формулами над F.
Множество функций (класс) называется замкнутым, если [F]=F.
Рассмотрим следующие классы функций.
1. Класс функций, сохраняющих 0:
 .
.
2. Класс функций, сохраняющих 1:

3. Класс самодвойственных функций:
 , где
, где 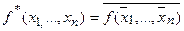 .
.
4. Класс монотонных функций
 где
где  .
.
5. Класс линейных функций
 , где + - означает сложение по модулю 2, а знак конъюнкции опущен.
, где + - означает сложение по модулю 2, а знак конъюнкции опущен.
Теорема. Классы Т0, Т1, Т*, ТМ, TL – замкнуты.
Доказательство. Чтобы доказать, что некоторый класс F замкнут достаточно показать, что, если формула реализована в виде формулы над F, то она принадлежит F.
Рассмотрим доказательство для одного класса функций Т0.
Пусть  и
и  . Тогда
. Тогда  .
.
Аналогичные доказательства можно привести для остальных классов.
Класс функций F называется полным, если его замыкание совпадает с Pn:
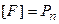 .
.
Другими словами, множество функций F образует полную систему, если любая функция реализуема в виде формулы над F.
Теорема.
Пусть заданы две системы функций 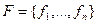 и
и  .
.
Тогда, если система F – полная и все функции из F реализуемы формулами над G, то система G тоже полная.
Доказательство. Пусть h – произвольная функция,  . Тогда [F]=Pn, следовательно, h реализуема формулой
. Тогда [F]=Pn, следовательно, h реализуема формулой 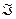 , базисом которой является F (
, базисом которой является F (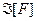 ). Если выполнить замену подформулы fi на подформулу
). Если выполнить замену подформулы fi на подформулу  в формуле
в формуле 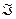 , то мы получим формулу над G.
, то мы получим формулу над G.
Следовательно, функция h реализуется формулой 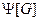 .
.
Примеры:
1. Система {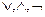 } – полная, т. к. любая логическая операция может быть выражена через дизъюнкцию, конъюнкцию и отрицание;
} – полная, т. к. любая логическая операция может быть выражена через дизъюнкцию, конъюнкцию и отрицание;
2. Система {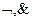 } – полная, т. к.
} – полная, т. к. 
3. Система { } – полная, т. к.
} – полная, т. к. 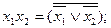
4. Система {|} – полная, т. к. 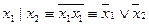 , а {
, а {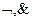 }и{
}и{ } – полные системы.
} – полные системы.
5. Система { } – полная, т. к.
} – полная, т. к.  Представление логической операции системой{
Представление логической операции системой{ }называется полиномом Жегалкина. Таким образом, всякая логическая операция представима в виде
}называется полиномом Жегалкина. Таким образом, всякая логическая операция представима в виде
 где
где  - сложение по модулю 2, знак · обозначает конъюнкцию,
- сложение по модулю 2, знак · обозначает конъюнкцию,  .
.
Теорема Поста: Система логических операций полна тогда и только тогда, когда она содержит хотя бы одну функцию, не сохраняющую 0, одну функцию, не сохраняющую 1, хотя бы одну несамодвойственную функцию, хотя бы одну нелинейную функцию и хотя бы одну немонотонную функцию.
Пример.
Докажем полноту системы {Å,Ú,1}.
| f | T0 | T1 | T* | TL | TM | В каждом столбце должен быть хотя бы один «-» |
| xÅy | + | - | - | + | - | |
| xÚy | + | + | - | - | + | |
| - | + | - | + | + |
1.
Проверка на принадлежность классу T0.


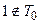
2.
Проверка на принадлежность классу T1.
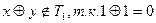
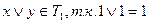

3.
Проверка на принадлежность классу T*.

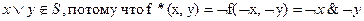
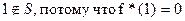
4.
Проверка на принадлежность классу TL.

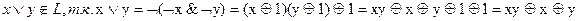
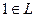
5.
Проверка на принадлежность классу TM.

f(0,0)=0
f(0,1)=1
f(1,0)=1
f(1,1)=0
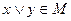
f(0,0)=0
f(0,1)=1
f(1,0)=1
f(1,1)=1

|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 343; Нарушение авторских прав?; Мы поможем в написании вашей работы!