Примеры тождественно истинных формул высказываний

· Закон тождества. «Всякое высказывание является логическим следованием себя самого»

x->x

Доказательство сводится к построению таблиц истинности

x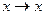

· Закон противоречия. «Для всякого высказывания неверно, что истинно и высказывание х и его отрицание.

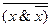
Доказательство сводится к построению таблиц истинности

x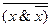

· Закон исключенного третьего. «Для каждого высказывания х истинно или само высказывание, или его отрицание»

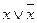
Доказательство сводится к построению таблиц истинности

x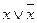

· Закон двойного отрицания. Отрицание от любого высказывания равносильно самому высказыванию.

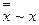
· Добавление антцедента (истина из чего угодно). Если х – истина, то для любого у истинно, что y->x.

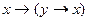
· Из ложного что угодно.

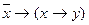
· Modus ponens. Если x->y – истинно и x – истинно, то согласно закону mp можно заключить, что истинно у.

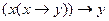
Этот тип заключения очень часто используется при математических доказательствах.

Пример.

1. Все простые числа, большие 2 – нечетны.

2. 7 – простое число.

3. Следовательно, 7- нечетное число.

Здесь применяются 2 закона. Первый закон – закон заключения от общего к частному будет рассмотрен в логике предикатов.

На основании этого закона преобразуется первая посылка заключения: Для всех х, если х – простое число большее 2, то х – нечетно. Согласно заключению от общего к частному высказывание если 7 – простое число большее 2, то 7 – нечетно – истинно. (А)

7 – нечетно (В)

A->B – Истинно

А – истинно

Применяем mp, следовательно, высказывание 7-нечетно – истинно.

· Modus tollens

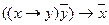
Или

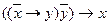
Этот закон применяется при доказательствах от противного. Он является двойственным к mp.

· Закон силлогизма

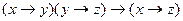
Этот закон позволяет строить сколь угодно длинные цепочки рассуждений.

Дата добавления: 2014-01-15