Зміна атмосферного тиску з висотою

З висотою атмосферний тиск зменшується, а також зменшується вище розташована маса атмосфери. Якби густина повітря з висотою не змінювалася, то тиск зменшувався б пропорційно висоті підняття. Але, як відомо, нижні шари повітря мають велику густину, ніж вище розташовані. Зниження атмосферного тиску з висотою повинно відбуватися не лінійно, а швидше у нижніх шарах і повільніше у верхніх.

Якщо виділити в атмосфері стовп повітря з поперечним перерізом 1 см² (рис. 2.1) і на будь-якому рівні АВ позначити тиск літерою p, то при зміні висоти на нескінченно малу величину ∆ z тиск зміниться на нескінченно малу величину ∆p. Таким чином, на рівні CD тиск буде дорівнювати p-∆p; зменшення тиску ∆p дорівнює масі об’єму повітря ABCD.

Рис. 2.1 Зміна тиску з висотою

Маса елементарного стовпа повітря ABCD дорівнює добутку об’єму, що рівний ∆z×1 см², на густину повітря в шарі ρ і на прискорення сили тяжіння g.

Звідси

(2.8)

Даний вираз називається основним рівнянням статики. Знак мінус показує, що тиск з висотою зменшується. Рівняння (2.8) виведене з припущення відсутності вертикальних і горизонтальних рухів, але все ж таки для реальних атмосферних умов воно справджується з високою точністю.

Для атмосфери в загальному вигляді неможливо вивести такого рівняння, яке б чітко виражало залежність тиску від висоти, тобто для різного розподілу температури чи густини повітря з висотою. Тому ця задача вирішується при деяких частинних припущеннях. Частинні розв’язки відповідають умовам, які характеризують окремі шари атмосфери та мають більш практичне значення.

1. Якщо густина повітря в атмосфері з висотою не змінюється, атмосферу називають однорідною. Висота такої атмосфери H записується у наступному вигляді:

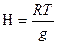(2.9)

За нормальних умов, тобто при температурі 273К (0^◦) і нормальній силі тяжіння 9,8 м/сек², отримаємо

Н₀ = 7991 м ≈ 8000 м

Висота однорідної атмосфери складає приблизно 8000 м. Для температури t, відмінної від 0⁰, отримаємо

. (2.10)

2. Якщо температура в атмосфері з висотою залишається постійною, то атмосфера називається ізотермічною. Висота такої атмосфери z дорівнює

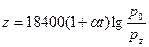, де (2.11)

p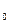 – тиск біля поверхні землі,

p_z – тиск на висоті z.

Користуючись цією формулою, можна знайти висоту, на якій тиск зменшується вдвічі, втричі і т.д. Для цього у формулу замість відношення 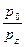підставляють відповідні значення. Наприклад, обчислимо, на якій висоті тиск зменшиться вдвоє при t=0⁰, z=18400·0,3=5500 м, тобто на кожні 5500 м тиск зменшується вдвічі.

3. Політропною називається така атмосфера, в якій температура змінюється з висотою лінійно, тобто градієнт температури γ з висотою залишається постійним:

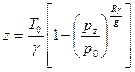(2.12)

4. Поняття стандартної атмосфери введено для різного роду практичних розрахунків. Для цієї умовної атмосфери приймають, що до висоти 11 км атмосфера політропна з градієнтом температури γ=0,65⁰/100 м; вище 11 км атмосфера ізотермічна.

Всі вище приведені формули не враховують зміну вологості з висотою, а також зміну сили тяжіння. Ці зміни враховуються повною барометричною формулою Лапласа, яка має наступний вигляд:

, де (2.13)

множник 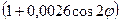характеризує зміну сили тяжіння в залежності від зміни широти місця,

множник визначає зміну сили тяжіння від висоти місця над рівнем моря,

h – висота в метрах,

е – середня пружність водяного пару (абсолютна вологість) повітряного стовпа між висотами 0 і z м,

р – середній тиск цього стовпа повітря,

φ – широта місця спостереження,

β – коефіцієнт, що дорівнює 0,314·10^-6 (для вільної атмосфери) та 0,196·10^-6 (для гірських місцевостей),

z – висота над рівнем моря середини стовпа повітря, що розглядається.

Якщо потрібно визначити зміну тиску з висотою для невеликих шарів атмосфери, використовують просту наближену формулу Бабіне. Її можна отримати, якщо рахувати густину повітря між двома висотними рівнями: постійною та рівною середній густині всього вертикального стовпа.

Уявно виділимо в атмосфері деякий стовп повітря (рис. 2.2) висотою h і з площею основи 1 см², тиск на нижньому рівні позначимо через p_н, а на верхньому через p_в.

Рис. 2.2 До виведення формули Бабіне

Різниця тисків p_н-p_в буде дорівнювати масі стовпа повітря з основою 1 см², висотою h і середньою густиною ρ, тобто p_н – p_в= ρgh, звідси 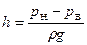. Але середня густина повітря ρ за рівнянням стану буде дорівнювати 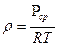, де р_ср - середній тиск між двома рівнями, дорівнює , а Т – середня температура. Звідси . Значить

, де (2.14)

=8000(1 + αt). Відповідно, можемо написати, що

(2.15)

Виведене рівняння і є формула Бабіне.

За допомогою барометричних формул Лапласа та Бабіне можливо вирішувати наступні задачі.

1. Визначення перевищення одного пункту над іншим, якщо відомі величини тиску p_н і p_в в цих пунктах і середня температура стовпа між ними. Такий розрахунок називається барометричним нівелюванням. Барометричне нівелювання менш точне, ніж геодезичне, але виконується воно значно простіше та швидше. Особливо часто барометричне нівелювання застосовується в гірських районах, непридатних для виконання геодезичних вимірювань. Визначення висоти по відліках тиску та температури виконують також і при аерологічному зондуванні атмосфери.

2. Знайти тиск p_в на відомій заданій висоті z, якщо відомо тиск внизу p_н і середня температура шару атмосфери t, що розглядається.

3. Визначити тиск на рівні моря p_н, якщо відомий тиск на верхньому рівні, висота пункту над рівнем моря та середня температура t шару атмосфери. Такий розрахунок називається приведенням тиску до рівня моря.

Приведення тиску до рівня моря проводиться на всіх метеорологічних станціях, передаючих синоптичні телеграми. Це необхідно для порівняння величини тиску на метеорологічних станціях, розміщених на різних висотах.

При вирішенні вказаних задач середню температуру можна визначати, знаючи температуру на одному з рівнів і використовуючи закон зміни температури з висотою.

Дата добавления: 2014-01-11