Характеристики завад

Рівень завад неможливо зробити рівним нулю. Крім того, на практиці зустрічається достатньо багато джерел завад, пов’язаних з несправностями або застосуванням несертифікованого устаткування.

Завади, як випадкові процеси, характеризуються законами розподілу, певним набором показників та функціями спектральної щільності потужності завад.

Закони розподілу визначаються видами завад (гаусів чи нормальний закон розподілу, закон розподілу білого шуму, закон розподілу Релея та т. інш.). Закони розподілу імовірності можуть бути представленими в диференціальному (щільність розподілу) і інтегральному вигляді.

Диференціальним видом нормального закону розподілу є щільність розподілу імовірності миттєвих значень і для найбільш розповсюджених гаусового та білого шумів це є нормальний закон розподілу (див. рис. 4а):

.

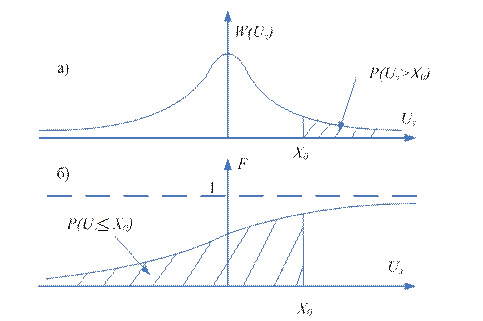
4. Щільність розподілу імовірності миттєвих значень для гаусового та білого шумів (диференціальний закон розподілу а)) та імовірність того, що завада не перевищить величину X₀ (інтегральний закон розподілу 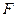– б))

Знаючи щільність розподілу імовірності миттєвих значень неважко визначити апостеріорну імовірність перевищення шумом деякого рівня X₀ (це може бути, наприклад, порогове значення для виявлення сигналу, див. рис. 4а):

.

Інтегральний вид закону розподілу 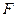дає можливість обрахувати імовірність того, що завада не перевищить величину X₀ (див. рис. 4б) і для цих же законів розподілу:

.

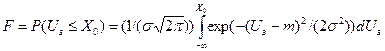Основними показниками завад (кількісними показниками завад) є їх інтенсивність (в основному для завад, які можна вважати імпульсними) та моменти першого та другого порядку.

Кількісні характеристики, дозволяють оцінити здатність завади, що “заважає”, тобто ступінь її впливу на переданий сигнал.

Інтенсивність імпульсів завади λ (чи середня частота проходження f_З) характеризує якість каналу, який забезпечує передачу тих чи інших інформаційних об’єктів, наприклад, сигналів чи повідомлень тривалістю . Тобто ця величина визначає кількість завад, які вплинуть на сигнал чи на повідомлення на часовому інтервалі .

Найчастіше як математичну модель імпульсної завади вибирають закон Пуассона:

,

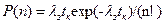де: P(n) – імовірність появи n імпульсів завади в сигналі чи в повідомленні на часовому інтервалі ;

n – кількість імпульсів завади, яка може спотворити сигнал чи повідомлення;

λ – інтенсивністьчи середня частота – f_З проходження імпульсів завади.

Величина P (n) тим менше, чим вище кратність завади, оскільки n! росте дуже швидко. Тому всі коди, що виявляють і/або виправляють спотворення, як правило, будуються з розрахунку появи невеликого числа спотворень, оскільки імовірність появи спотворень великої кратності дуже мала.

Відзначимо, що канал зв’язку, в якому діє імпульсна завада, можна описувати по-різному. Модель Пуассона – лише один з варіантів. Вона не описує всі можливі ситуації, що виникають в такому каналі зв’язку.

Слід докладніше розглянути величину f_З. Її можна вважати інтенсивністю завади λ тільки при однаковій тривалості часового інтервалу. Інакше ситуація не буде відбита адекватно.

Важливою характеристикою є середня кількість спотворень i = λ _З в сигналі тривалістю .

Всі системи передачі залежно від величини i можна розділити на три групи.

§ i << 1 характерний для систем, що працюють в умовах дії імпульсних завад малої інтенсивності.

§ i = 1 … 3 має місце в системах, що працюють в умовах дії імпульсних завад середньої інтенсивності. При цьому будь-яка передача повідомлення може супроводжуватися спотворенням. i = 3 – суб’єктивна межа, проте говорити про більшу величину нераціонально, оскільки в подібному випадку довелося б застосовувати коди, що виправляють більше трьох помилок. Застосування ж таких кодів вимагає невиправданих апаратурних витрат.

§ i > 3 для систем, що працюють в умовах завад великої інтенсивності. У таких системах, можливо, діє спеціально організована завада. В рамках даного курсу ці системи розглянуті не будуть.

Момент першого порядку (перший момент):

,

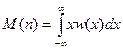де ω (х) – щільність розподілу, виражає математичне очікування, або постійну складову процесу.

Центральний момент другого порядку називається дисперсією і дорівнює:

Дисперсія виражає потужність змінної складової, а середній квадрат M (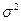) – загальну потужність. В більшості випадків 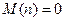, так що дисперсія співпадає з середнім квадратом.

2.2. Деякі види шумів

2.2.1. Гаусів шум

Гаусів шум, або гаусів випадковий процес, виникає при підсумовуванні статистично незалежних білих шумів (див. нижче). Він переважає в практичних завданнях. Випадковий процес x(t) називається гаусовим, якщо для будь-якого набору фіксованих моментів часу t_n випадкові величини x_n підкоряються нормальному розподілу. Щільність розподілу імовірності миттєвих значень x(t) процесу Гауса визначається виразом:

,

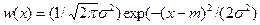де: m – середнє значення;

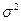– стандартне (середньоквадратичне) відхилення.

Середнє значення для розподілу Гауса дорівнює математичному очікуванню, яке, в свою чергу, дорівнює нулю:

Стандартне (середньоквадратичне) відхилення:

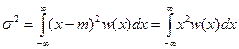
Отже, щільність імовірності гаусова процесу повністю характеризується спектральною щільністю, по якій можна визначити значення дисперсії процесу. На рисунку 5 показана залежність форми розподілу Гауса від середньоквадратичного відхилення. Звернемо увагу на те, що завада малої амплітуди є більш імовірною, ніж завада великої амплітуди.

5. Залежність форми розподілу Гауса від середньоквадратичного відхилення.

2.2.2. Білий шум

Білий шум – стаціонарний шум, спектральні складові якого рівномірно розподілені по всьому діапазону частот.

У природі й техніці “чисто” білий шум (тобто білий шум, що має однакову спектральну потужність на всіх частотах) не зустрічається (через те, що такий сигнал мав би нескінченну потужність), однак під категорію білих шумів попадають будь-які шуми, спектральна щільність яких однакова (або майже однакова) у даному діапазоні частот.

Білий шум є різновидом завад із розподілом Гауса із з необмеженим набором частот та рівномірним спектром, тобто спектральна щільність потужності завади

.

Як модель, шум із такою властивістю є найбільш поширеним і називається білим шумом. Потужність білого шуму в смузі Δ f рівна

,

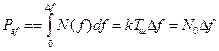Таким чином, N₀ = ,

де: k – постійна Больцмана – фізична постійна, така, що визначає зв’язок між температурою і енергією. Її експериментальне значення в системі СІ дорівнює:

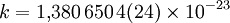Дж/К,

К – градус (Кельвіна). Числа в круглих дужках указують стандартну погрішність в останніх цифрах значення величини;

3. Поняття про модуляцію. Види модуляції

Як уже відомо, повідомлення передаються за допомогою сигналів. Інформація, яку переносять сигнали, зосереджена в змінах параметрів несущого сигналу.

Зміну параметрів несущого сигналу відповідно до параметрів інформаційного сигналу (накладення інформаційного сигналу на несущий) називають модуляцією.

Модуляція [лат. modulatio – мірність, розмірність] – процес зміни одного або декількох параметрів високочастотного модульованого коливання за законом інформаційного низькочастотного повідомлення (сигналу). Це процес “переносу” інформаційного сигналу на ту частоту, що апріорі відома як несуча. Як такі можуть бути використані коливання різної форми (прямокутні, трикутні і т. д.), проте найчастіше застосовуються гармонійні коливання. Залежно від того, який з параметрів коливання, що несе, змінюється, розрізняють види модуляції (амплітудна, частотна, фазова і ін.). Модуляція дискретним сигналом називається цифровою модуляцією або маніпуляцією.

Загальний принцип модуляції полягає в зміні одного або декількох параметрів несучого коливання (переносника)

f (а, b,..., t)

відповідно до переданого повідомлення. Так, наприклад, коли як переносник обрано гармонійне коливання

f (t) = U₀ cos(ω ₀ t + φ),

то можна утворити три види модуляції: амплітудну (АМ), частотну (ЧМ) і фазову (ФМ).

У випадку застосування аналогових каналів передачі даних переносниками інформації є гармонійні коливання (несучі) з несучою частотою ω_н. Щоб дане коливання було несучим, необхідно виконати дві умови:

1) середовище поширення сигналу повинна добре пропускати коливання із частотою ω_н;

2) частота несучої повинна бути багато більше верхньої частоти в спектрі переданого повідомлення, тобто ω_н >> Ω_н, де Ω_н = 2π F_m, F_m – верхня частота в спектрі повідомлення.

Друга умова випливає з вимоги, щоб за один період несучого коливання параметр, що модулюється, змінився незначно. Інакше виникнуть спотворення.

Якщо переносником є періодична послідовність імпульсів, то при заданій формі імпульсів f ₀(t) можна утворити чотири основних види імпульсної модуляції: амплітудноімпульсну (АІМ), широтно-імпульсну (ШІМ), фазо-імпульсну (ФІМ) і частотно-імпульсну (ЧІМ). Застосування радіоімпульсів дозволяє одержати ще два види модуляції: по частоті і по фазі високочастотного заповнення.

Найбільшого поширення набули модуляція гармонійних сигналів, як несучих, і модуляція із використанням періодичних послідовностей імпульсів.

Формально, якщо інформаційний сигнал (повідомлення) позначити s (t), сигнал-переносник, параметр якого змінюється відповідно до повідомлення, як p(t), то при модуляції виконується перетворення цих двох сигналів в один модульований сигнал U (t) відповідно до рівняння

,

де 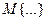– оператор, визначуваний видом модуляції. Для виділення повідомлення s (t) на приймальній стороні необхідно виконати зворотне перетворення (демодуляцію), тобто

.

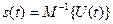Залежно від вигляду, функціональної форми і числа параметрів сигналу-переносника р (t) і інформаційного сигналу s (t) варіюються властивості різних методів модуляції, а саме, вигляд і ширина спектру сигналу U (t), стійкість до дії завад і так далі.

Якщо інформаційний параметр сигналу-переносника змінюється безперервно, то методи модуляції є безперервними (поширені, наприклад, методи амплітудної, фазової і частотної безперервної модуляції гармонійного сигналу-переносника).

Якщо як сигнал-переносник використовують періодичну послідовність імпульсів, тоді модуляцію називають імпульсною чи дискретною (наприклад, при зміні амплітуди або частоти імпульсів згідно із законом s (t) має місце амплітудноімпульсна або частотно-імпульсна модуляція відповідно).

4. Амплітудна модуляція

Амплітудна модуляція гармонійних коливань

Амплітудно-модульований (АМ) сигнал в загальному випадку визначається виразом

,

де: s (t) – інформаційний сигнал (що модулює), p(t) – сигнал-переносник, m – коефіцієнт модуляції.

Оскільки, в найпростішому випадку, спектри обох сигналів є поодинокими гармоніками, то спектри сигналів при такій модуляції мають вигляд, наданий на рис. 6 і, як відомо, утворюються перенесенням спектру інформаційного сигналу в область частоти сигналу-переносника.

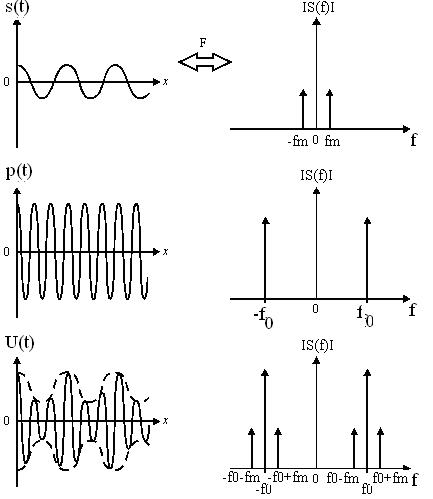
6. Спектр гармонійного сигналу з гармонійною АМ модуляцією

Дискретна модуляція. Багаторівнева амплітудна маніпуляція

Перш ніж розглядати власне методи модуляції в системах зв’язку, розглянемо основні способи представлення сигналів, прийняті для опису методів модуляції.

Надалі врахуємо те, що найбільш застосовним в сучасних інформаційно – телекомунікаційних системах є передача чи зберігання дискретної (цифрової) інформації. При цьому інформаційний параметр може приймати обмежену кількість значень, а така модуляція має назву дискретної. Якщо значення параметра закодовані і передаються в цифровій формі, то відповідні види модуляції носять назву цифрової модуляції. До дискретних видів модуляції відносяться, наприклад, амплітудна, частотна і фазова маніпуляції.

На рис. 7 показані приклади АМ, ЧМ і ФМ для випадку, коли гармоніка модулюється послідовністю імпульсів (нагадаємо, такий різновид модуляції називають маніпуляцією), коли сигнал є бінарним, тобто може приймати значення “0” чи “1”.

7. Приклади АМ, ЧМ і ФМ, коли модулюючим сигналом є послідовність імпульсів

Як відомо, дискретні сигнали можуть бути бінарними або багаторівневими (багатопозиційними) (рис. 8).

8. Види дискретних сигналів (бінарні та багатопозиційні)

Передача багаторівневих сигналів здійснюється послідовністю бінарних сигналів із різними амплітудами (рис. 9).

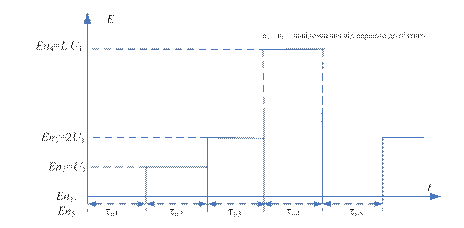
9. Формування багаторівневого сигналу (Еп₁= Еп₅ =0 – рівні першого та п’ятого повідомлень, Еп₂, Еп₃, Еп₄ – рівні 2, 3 та 4 – го повідомлень,
Еп₄ = 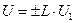– рівень четвертого повідомлення)

Частотні характеристики спектрів цих сигналів однакові і, як відомо, утворюються перенесенням спектру інформаційного сигналу в область частоти сигналу-переносника. Обгинаюча спектру інформаційного сигналу є функцією типу 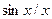, в наслідок чого мають вигляд, наданий на рис. 10.

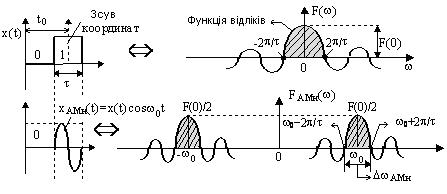
10. Спектр при амплітудній маніпуляції

Швидкість передачі двійкових символів у вигляді радіоімпульсів (як і при передачі відеоімпульсів така швидкість має назву швидкості посимвольної передачі) визначається як 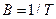і, при прагненні досягти максимального її значення при Т → τ, приймає значення .

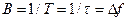Отже, при амплітудній маніпуляції при передачі дворівневих сигналів (кількість рівнів амплітудної модуляції m = 2, коли при передачі “1” сигнал приймає одно з двох значень – 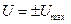, а інакше ), швидкість передачі інформації V дорівнює швидкості посимвольної передачі, яка необхідна для передачі однорівневого АМ радіосигналу, що чисельно дорівнює смузі частот П_АМ:

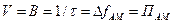. (2)

В цих виразах враховано, що 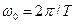і, відповідно, , де: 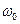,– основна частота сигналу, якою модульовано відеосигнал.

Зрозуміло, що при передачі багаторівневих сигналів (кількість рівнів амплітудної модуляції m > 2), наприклад, при передачі одного із сигналів із рівнем 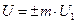(див. рис. 9), де – найменший рівень сигналу, відмінного від “0”, сигнал приймає одне з m значень. Кількість розрядів, яка потрібна для представлення цих m значень, враховуючи рівень “0”, дорівнює 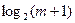, отже, за рахунок того, що при передачі одного символу передається 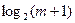розрядів, швидкість передачі інформації зростає від до:

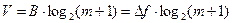. (3)

Звернемо увагу на те, що цей вираз є справедливим і при використанні однорівневих сигналів. Дійсно, в цьому випадку (m = 2), вираз (3) набуває вигляду:

,

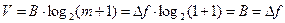що збігається із виразом (2).

Дата добавления: 2014-01-11