
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Наращение по простой процентной ставке
|
|
|
|
Формула наращения. Под наращенной суммой ссуды (долга, депозита и т.п.) понимают первоначальную ее сумму с начисленными процентами к концу срока. Наращенная сумма определяется умножением первоначальной суммы долга на множитель наращения, который показывает, во сколько раз наращенная сумма больше первоначальной.
Введем обозначения:
 - проценты за весь срок ссуды;
- проценты за весь срок ссуды;
 - первоначальная сумма долга;
- первоначальная сумма долга;
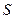 - наращенная сумма, или сумма в конце срока;
- наращенная сумма, или сумма в конце срока;
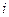 - ставка наращения (десятичная дробь);
- ставка наращения (десятичная дробь);
 - срок ссуды.
- срок ссуды.
Срок обычно измеряется в годах; соответственно 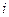 - годовая ставка. Каждый год приносит проценты в сумме
- годовая ставка. Каждый год приносит проценты в сумме 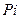 . Начисленные за весь срок проценты составят
. Начисленные за весь срок проценты составят
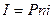
Наращенная сумма
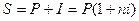 (1.1)
(1.1)
Эту формулу называют формулой простых процентов, а множитель - множителем наращения простых процентов. График роста по простым процентам представлен на рис. 1.1.
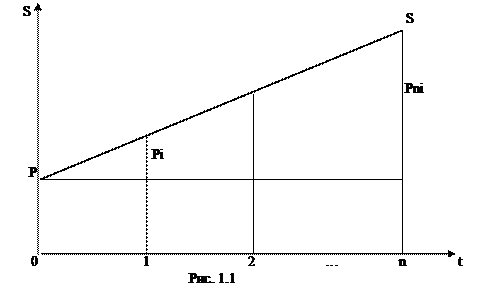
Расчет процентов для краткосрочных ссуд. Обычно к наращению по простым процентам прибегают при выдаче краткосрочных ссуд (на срок до одного года) или в случаях, когда проценты не присоединяются к сумме долга, а периодически выплачиваются кредитору. Поскольку в контракте обычно фиксируется годовая ставка, то при сроке ссуды менее года необходимо определить, какая часть годового процента уплачивается кредитору.
Выразим общий срок ссуды в виде дроби:
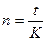 ,
,
где 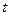 - число дней ссуды;
- число дней ссуды;
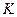 - число дней в году, или временная база.
- число дней в году, или временная база.
Если 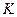 = 360 (12 месяцев по 30 дней), то получают обыкновенные проценты, а при использовании действительной продолжительности года получают точные проценты.
= 360 (12 месяцев по 30 дней), то получают обыкновенные проценты, а при использовании действительной продолжительности года получают точные проценты.
Число дней ссуды также можно измерить приближенно и точно. В первом случае считается, что любой месяц содержит 30 дней. Точное число дней ссуды определяется подсчетом числа дней между датой выдачи ссуды и датой ее погашения. День выдачи и день погашения считаются за один день.
На практике применяются три варианта расчета простых процентов:
а) точные проценты с точным числом дней ссуды. Этот вариант дает самые точные результаты и обозначается 365/365.
б) обыкновенные проценты с точным числом дней ссуды. Этот метод также называется банковским и обозначается 365/360.
в) обыкновенные проценты с приближенным числом дней ссуды. Применяется при промежуточных расчетах и обозначается 360/360.
Пример 1.1.Ссуда в размере 1000 руб. выдана 1 марта до 1 июня под 20% годовых. Какую сумму должен заплатить должник в конце срока?
Число дней ссуды: точное - 92, приближенное - 90.
1. Точные проценты с точным числом дней ссуды (365/365):
 руб.
2. Обыкновенные проценты с точным числом дней ссуды (365/360): руб.
2. Обыкновенные проценты с точным числом дней ссуды (365/360):
 руб.
3. Обыкновенные проценты с приближенным числом дней ссуды (360/360): руб.
3. Обыкновенные проценты с приближенным числом дней ссуды (360/360):
 руб. руб.
|
Переменные ставки. В кредитных соглашениях иногда предусматриваются изменяющиеся во времени процентные ставки. При простых ставках наращения на конец срока сумма
 , (1.2)
, (1.2)
где 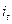 - ставка простых процентов в периоде
- ставка простых процентов в периоде 

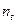 - продолжительность периода,
- продолжительность периода, 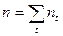 .
.
Пример 1.2.Контракт предусматривает начисление процентов: первый год - ставка 16%, в каждом последующем полугодии ставка повышается на 1%. Необходимо определить множитель наращения за 2,5 года.
 
|
банки практикуют начисление и выплату процентов ежеквартально или ежемесячно, причем начисление производится по постоянной или растущей процентной ставке. Для этого в контракте фиксируются годовые ставки, по которым определяются размеры квартальных или месячных ставок. Годовые ставки в этом случае называют номинальными. Например: банк предлагает следующие номинальные ставки для поквартального начисления и выплаты процентов: 20, 24, 28, 32%. Т.о. за первый квартал выплачивается 20/4 = 5%, за второй 24/4 = 6% и т.д.
Реинвестирование. В практике при инвестировании средств в краткосрочные депозиты иногда прибегают к неоднократному последовательному повторению наращения по простым процентам в пределах заданного общего срока, т.е. к реинвестированию полученных на каждом этапе наращения средств. Наращенная сумма для всего срока составит
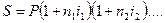 (1.3)
(1.3)
где  - ставки, по которым производится реинвестирование.
- ставки, по которым производится реинвестирование.
Если периоды начисления и ставки не изменяются во времени, то
 , (1.4)
, (1.4)
где 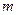 - количество реинвестиций.
- количество реинвестиций.
Пример 1.3.100 руб. положены 1 января на месячный депозит под 20% годовых. Какова наращенная сумма, если операция повторяется три раза? Если начислять точные проценты, то
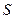 = 100(1 + = 100(1 + 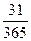 0,2)(1 + 0,2)(1 +  0,2)(1 + 0,2)(1 + 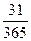 0,2) = 105,01 руб.
Начисление обыкновенных процентов дает 0,2) = 105,01 руб.
Начисление обыкновенных процентов дает
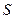 = 100(1 + = 100(1 +  0,2)3 = 105,08 руб. 0,2)3 = 105,08 руб.
|
|
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 941; Нарушение авторских прав?; Мы поможем в написании вашей работы!