
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Наращение по сложной процентной ставке
|
|
|
|
Формула наращения. В средне- и долгосрочных финансово-кредитных операциях обычно процентыприсоединяются к сумме долга, а для наращения применяют сложные проценты. Присоединение начисленных процентов к сумме, которая служила базой для их начисления, называется капитализацией процентов.
Запишем формулу для расчета наращенной суммы при условии, что проценты начисляются и капитализируются один раз в году.
Очевидно, что в конце первого года проценты равны 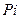 , а наращенная сумма составит
, а наращенная сумма составит 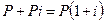 . К концу второго года она достигает величины
. К концу второго года она достигает величины  и т.д.
и т.д.
В конце n-го года она будет
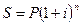 (1.8)
(1.8)
Проценты за этот же период равны
 (1.9)
(1.9)
Проценты за каждый последовательный год увеличиваются. Для некоторого промежуточного года t они равны
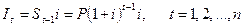 (1.10)
(1.10)
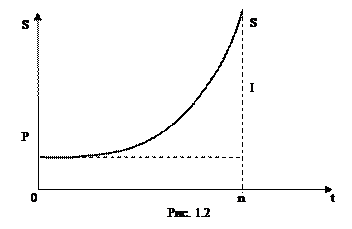 Графическая иллюстрация роста по сложным процентам на рис. 1.2. Величину
Графическая иллюстрация роста по сложным процентам на рис. 1.2. Величину 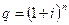 называют множителем наращения по сложным процентам.
называют множителем наращения по сложным процентам.
Пример 1.7.Какой величины достигнет долг, равный 1000 рублей, через 4 года при росте по сложной ставке 15% годовых?
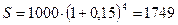 руб. руб.
|
Формула (1.8) получена для годовой процентной ставки и срока в годах. Однако ее можно применять и при других периодах начисления. В этих случаях 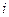 - ставка за период начисления,
- ставка за период начисления,  - число таких периодов.
- число таких периодов.
Переменные ставки. Еслизначения переменных ставок фиксируются в контракте, получаем
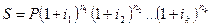 ,
,
где 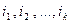 - последовательные во времени значения ставок;
- последовательные во времени значения ставок;
 - соответствующие этим ставкам периоды.
- соответствующие этим ставкам периоды.
Пример 1.8.Срок ссуды - 5 лет, договорная процентная ставка – 12% годовых в первые два года и 15% - в оставшиеся. Множитель наращения в этом случае
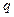 = (1 + 0,12)2(1 + 0,15)3= 1,9078 = (1 + 0,12)2(1 + 0,15)3= 1,9078
|
Рост по сложным и простым процентам. Для сопоставления результатов наращения достаточно сравнить соответствующие множители наращения. Для ставки простых процентов введем индекс 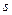 . Получим следующие соотношения множителей наращения:
. Получим следующие соотношения множителей наращения:
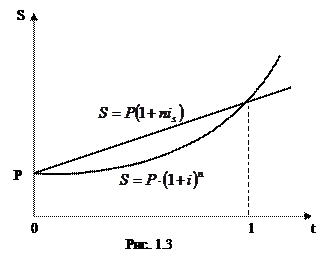
срок меньше года  ;
;
срок равен году  ;
;
срок больше года 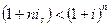 .
.
Графическая иллюстрация соотношения множителей наращения приведена на рис. 1.3.
|
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 536; Нарушение авторских прав?; Мы поможем в написании вашей работы!