
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Инфляция
|
|
|
|
В рассмотренных нами методах наращения не учитывалось снижение реальной покупательной способности денег за период, охватываемый финансовой операцией. Однако инфляция может играть заметную роль.
Рост цен за некоторый период измеряется с помощью индекса цен 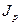 . Пусть
. Пусть 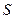 - наращенная сумма денег. С учетом инфляции она составит:
- наращенная сумма денег. С учетом инфляции она составит:
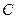 =
= 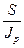 . (2.6)
. (2.6)
Свяжем индекс цен и темп инфляции. Под темпом инфляции понимают относительный прирост цен за период. Обозначим его 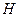 , и будем измерять в процентах (в формулы будем подставлять в виде десятичной дроби).
, и будем измерять в процентах (в формулы будем подставлять в виде десятичной дроби).
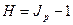 . (2.7)
. (2.7)
В свою очередь
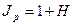 . (2.8)
. (2.8)
Например, если темп инфляции равен 130%, то цены за этот период выросли в 2,3 раза.
Среднегодовой темп роста цен 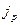 находится на основе
находится на основе 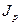 как
как

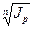 , (2.9)
, (2.9)
Поскольку инфляция является цепным процессом (цены в текущем периоде повышаются на 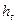 процентов относительно уровня предыдущего периода), то индекс цен за несколько таких периодов равен:
процентов относительно уровня предыдущего периода), то индекс цен за несколько таких периодов равен:
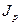 =
=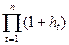 (2.10)
(2.10)
Если 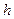 - постоянный темп инфляции за период, то за
- постоянный темп инфляции за период, то за  таких периодов получим
таких периодов получим
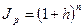 . (2.11)
. (2.11)
Пример 2.6.Постоянный темп инфляции на уровне 5% в месяц за год приведет к росту цен в размере 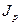 = 1,0512 = 1,796
т.о. годовой темп инфляции = 1,0512 = 1,796
т.о. годовой темп инфляции 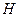 = 1,796 - 1 = 0,796 или 79,6%, а не 60%. = 1,796 - 1 = 0,796 или 79,6%, а не 60%.
|
Пример 2.7.Последовательный прирост цен по месяцам составил 5, 10 и 8%. Индекс цен за три месяца (2.10) равен 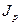 = 1,05x1,1x1,08 = 1,25.
Темп инфляции за три месяца составил 25%. = 1,05x1,1x1,08 = 1,25.
Темп инфляции за три месяца составил 25%.
|
Если наращение производится по простой ставке:
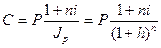 (2.12)
(2.12)
увеличение наращенной суммы, с учетом сохранения покупательной способности денег, имеет место если 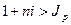 .
.
| Пример 2.8.Допустим, на сумму 1,5 млн руб. в течение 3 месяцев начисляются простые проценты по ставке 30% годовых (К = 360). Наращенная сумма равна 1,6125 млн.руб. Если ежемесячная инфляция характеризуется темпами из примера 2.7, то наращенная сумма с учетом инфляции составит 1,6125/1,25 = 1,29 млн.руб. |
Пусть наращение производится по сложным процентам. Тогда
 (2.13)
(2.13)
Определим при какой процентной ставке наращение будет только компенсировать инфляцию? В случае простых процентов множитель наращения с учетом инфляции из (2.12) должен быть равен 1. Отсюда минимально допустимая ставка:
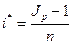 (2.14)
(2.14)
Аналогично из (2.13) для сложных процентов
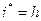 (2.15)
(2.15)
Ставку, превышающую  , называют положительной процентной ставкой.
, называют положительной процентной ставкой.
Пример 2.9.По данным примера 2.7 найдем минимально допустимую величину ставки. 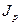 = 1,25 за три месяца. = 1,25 за три месяца.
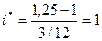 или 100 % годовых. или 100 % годовых.
|
|
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 967; Нарушение авторских прав?; Мы поможем в написании вашей работы!