Теореми Шеннона. Підвищення пропускної спроможності безперервного каналу шляхом прямого розширення смуги пропускання каналу

Найбільш відомими та придатними для подальшого аналізу є три наступних теореми Шеннона.

Перша теорема визначає умови кодування повідомлень для дискретних каналів без завад і формулюється наступним чином:

якщо продуктивність джереласкільки завгодно близька до пропускної спроможності каналу 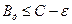, де 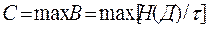– пропускна спроможність каналу, 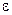– скільки завгодно мала величина, то завжди існує спосіб кодування, що дозволяє передавати по каналу всі повідомлення джерела; передачу всіх повідомлень при 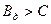здійснити неможливо.

Сенс теореми зводиться до того, що, як би не була велика надмірність джерела, всі його повідомлення можуть бути передані по каналу, якщо .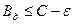

Друга теорема Шеннона визначає умови кодування повідомлень для дискретних каналів з завадами: якщо продуктивність джерела скільки завгодно близька до пропускної спроможності каналу 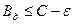, де 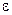– скільки завгодно мала величина, то існує спосіб кодування, що дозволяє передавати по каналу всі повідомлення джерела із скільки завгодно малою вірогідністю помилки; така передача всіх повідомлень при 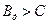неможлива.

Третя теорема Шеннона визначає умови передачі безперервних повідомлень для безперервних каналів з завадами: якщо при заданій середньоквадратичній погрішності 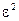оцінки повідомлень джерела його продуктивність 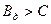, то існує спосіб кодування, що дозволяє передавати всі безперервні повідомлення джерела з помилкою у відтворенні на виході каналу, що скільки завгодно мало відрізняється від .

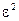Якщо вважати, що сигнал і завада незалежні і мають нормальний розподіл, то ця теорема трансформується в знамениту формулу Шеннона для пропускної спроможності каналу, яка має вид:

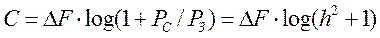, 1)

де: 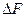– смуга пропускання каналу, 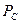, 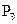– потужність сигналу і завади (співвідношення 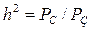характеризує, як вже наголошувалося раніше, параметр сигнал/завада).

Із цього виразу витікає, що пропускна спроможність безперервного каналу з завадами:

- зростає зі збільшенням ширини смуги частот каналу f_m;

- зростає зі збільшенням відношення корисний сигнал/завада (у цьому випадку сигнал буде впевнено розпізнаватися на фоні завад);

- не дорівнює нулю навіть при Р_С << Р_З (тобто, передачу інформації принципово можна вести сигналами більш слабкими, ніж завади).

Вважається, що формула (1) указує граничне значення пропускної спроможності каналу, якого досягти вельми важко, до нього можна лише наблизитися. При виводі цієї формули передбачалося, що на приймальній стороні сигнали повністю відділяються від завад (шумів). Враховуючи нереальність цього припущення, в реальних системах важко очікувати результатів, близьких до (1).

Із виразу (1) видно, що одним із чинників, яким можна впливати на пропускну спроможність 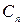є ширина смуги пропускання каналу передачі даних 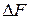. Відомим є аналіз того, що шлях збільшення пропускної спроможності за рахунок розширення смуги пропускання каналу є найефективнішим.

Неважко показати, що розширення смуги пропускання каналу можна досягти принаймні двома способами. Перший із них, назвемо його способом прямого (безпосереднього) розширення смуги пропускання, полягає в підвищенні швидкості посимвольного обміну В, що можливе, зрозуміло, за рахунок зменшення періоду, а також тривалості символів, якими здійснюється обмін. При цьому згідно із теоремою Котельникова при організації передачі двійкових послідовностей в безперервних каналах для забезпечення приймання сигналів із прийнятною якістю потрібно забезпечити ширину смугу пропускання приймача 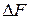такою, що 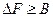, де В – швидкість посимвольної передачі інформації. Тоді потужність завади на вході приймача може бути визначена через однобічну спектральну щільність потужності завади – N ₀ та ширину смуги пропускання приймача :

.

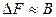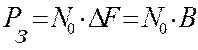Отже,

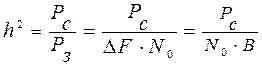. (3)

В наслідок викладеного відмітимо, що в разі організації обміну інформацією у вигляді двійкових послідовностей при ширині смуги пропускання приймача 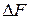такій, що 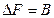, можна записати

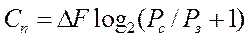. (4)

Із розглянутих виразів може скластися враження, начебто пропускну спроможність можна збільшувати необмежено за рахунок збільшення ширини смуги пропускання 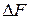чи швидкості посимвольної передачі інформації В. Покажемо, що останнє твердження має певні вади. З цією метою врахуємо, що наявні в каналі передачі даних завади можуть бути описаними через спектральну щільність потужності 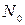. В цьому разі вираз (4) із урахуванням (3) можна надати у наступному вигляді:

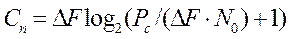. (5)

Із виразу (5) видно, що твердження відносно можливості необмежено збільшувати пропускну спроможність 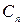за рахунок збільшення швидкості посимвольної передачі інформації В, а отже, розширення смуги пропускання 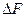, є не таким і очевидним, оскільки збільшення одного із множників 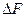призводить до зменшення іншого – підлогаріфмічного виразу.

Дослідження показують, що таке збільшення має границю у вигляді:

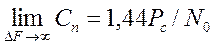, (7)

чи:

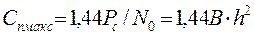, (8)

де 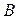– швидкість посимвольної передачі інформації в каналі, при якій зафіксоване співвідношення сигнал/завада дорівнює .

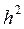Дата добавления: 2014-01-11