Лекция 2. Классификация систем управления

Классификация систем управления

В соответствии с приведенными выше аспектами управления можно классифицировать системы управления:

– по информационному признаку;

– по типу сигналов;

– по алгоритмическому признаку;

– по энергетическому признаку.

Классификация по информационному признаку. Управление и информация – понятия, неразрывно связанные между собой. Для управления необходима информация:

– о целях управления;

– о возмущениях среды;

– о состоянии объекта управления;

– о характеристиках объекта.

Характер и полноту доступной информации определяют различные принципы управления. В качестве таких принципов используются:

– принцип разомкнутого управления;

– принцип обратной связи;

– принцип адаптивного управления.

Принцип разомкнутого управления используется при наличии полной априорной информации о целях управления и характеристиках объекта и отсутствии возмущающих воздействий. Если

цель управления задана в виде

,

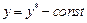т.е. цель управления состоит в поддержании выходного параметра неизменным, то требуемый уровень управляющего воздействия легко определяется по статической характеристике объекта. Системы этого типа носят название систем стабилизации.

Этот принцип реализуется в виде нескольких разновидностей. К ним относятся:

1. Системы с программным управлением, в которых целью управления является изменение управляемой переменной y по определенной программе, заданной в виде функции времени y (t), например, программа набора высоты самолетом, программа изменения температуры в печи и т.д. Здесь для определения оптимального управляющего воздействия u *(t) необходимо знать динамические характеристики объекта управления. При этом оптимальное управление возможно не всегда.

2. Системы с компенсацией возмущений. Возмущения f (t) – это воздействия среды на объект (причина), вызывающие отклонения управляемой переменной от заданных значений (программ изменения). При наличии полной информации о возмущениях она может быть учтена при расчете оптимального управления. Если же доступна только текущая информация (т.е. ее можно измерить) о возмущениях, то ее можно компенсировать путем дополнительного воздействия на объект, суммируя его с управляющим воздействием, как показано на рис.1.5.

Рис. 1.5. Разомкнутая система с компенсацией возмущения

Алгоритм обработки текущей информации о возмущении f в компенсаторе K для вычисления компенсирующего возмущения d u_f строится на основе характеристик объекта по каналам управления и возмущения.

Для работоспособности такой системы необходимы устойчивость режима работы объекта, а другие (некомпенсируемые) возмущения должны быть слабыми.

Принцип обратной связи устраняет недостатки разомкнутых систем. Дело в том, что практически невозможно учесть информацию обо всех (в первую очередь о неизвестных) возмущениях, действующих на объект. Проще использовать информацию о последствиях возмущений, т.е. об отклонениях управляемой переменной, вызванных всеми возмущениями. Эта задача и решается на основе принципа обратной связи. Структура системы управления с обратной связью показана на рис.1.6.

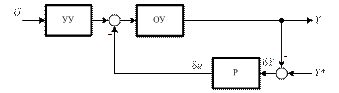
Рис.1.6. Структура системы управления с обратной связью

Здесь исходная информация о цели в виде задающего воздействия y *(t) сравнивается с текущим значением y (t) управляемой переменной. Результат сравнения в виде отклонения d y поступает на регулятор Р, вырабатывающий дополнительное управляющее воздействие d u, направленное на уменьшение этого отклонения. Полученное воздействие складывается с исходным (запланированным априорно) управляющим воздействием u *, в результате чего формируется текущее воздействие u. Подобные системы называются следящими.

Обратная связь является единственным средством стабилизации неустойчивых режимов работы. Кроме того, обратная связь позволяет уменьшить влияние изменений характеристик объекта на свойства системы в целом. Таким образом, важнейшим достоинством принципа обратной связи является его универсальность. Недостатком его является недостижимость абсолютной инвариантности (нечувствительности) к произвольным воздействиям: для формирования сигнала управления u принципиально необходимы отклонения d y, являющиеся входной информацией устройства управления.

Комбинированным вариантом реализации разомкнутого и замкнутого принципов управления являются системы с обратной связью и компенсацией параметрических возмущений. Структура такой системы приведена на рис. 1.7.

Здесь внешние возмущения воздействуют не только на объект управления, но и на компенсатор K, вырабатывающий новые значения параметров настройки регулятора, либо меняющий алгоритм его работы.

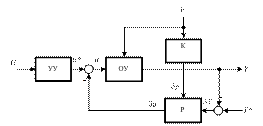
Рис. 1.7. Структура системы с обратной связью и компенсацией

параметрических возмущений

Примером подобной системы управления являются некоторые автопилоты. Поскольку аэродинамические характеристики самолета меняются с высотой, то параметры автопилота можно подстраивать, измеряя барометрическое давление.

Отметим, что по отношению к параметрическим воздействиям такие системы являются разомкнутыми: управление здесь осуществляется по причине, а не по следствию. Это позволяет достичь абсолютной инвариантности их характеристик к параметрическим возмущениям.

Принцип адаптивного управления состоит в том, что устройства управления или регуляторы подстраиваются на основе текущих изменений свойств объекта. Целью адаптивной системы является оптимизация показателей качества, т.е. поиск экстремума некоторого функционала (см. далее).

Структура системы управления, реализующая этот принцип, приведена на рис. 1.8.

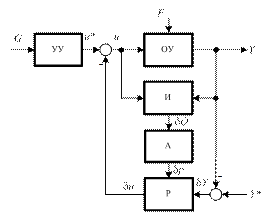
Рис. 1.8. Адаптивная система управления

Изменения свойств объекта отслеживаются идентификатором И, информация с выхода которого снимается в виде отклонения характеристик объекта d O, поступающего на блок адаптации А. На основе этой информации блок адаптации вычисляет новые значения параметров регулятора Р. В результате реализуется принцип отрицательной параметрической связи, т.е. образуется замкнутый контур передачи и обработки информации для компенсации параметрических возмущений среды. Отметим также, что основной контур управления (объект – регулятор) можно рассматривать как объект управления системы более высокого порядка: управляющим воздействием системы второго уровня являются изменения параметров регулятора системы первого уровня, а возмущением – параметрические воздействия среды. Идентификатор И является измерительным элементом в системе второго уровня, а регулятором является блок настройки А.Адаптивные системы подразделяются на системы экстремального управления и системы оптимального управления.

Системы экстремального управления решают задачу поддержания экстремума значения управляемой величины. Для этой цели на объект подаются пробные воздействия для определения знака изменения управляемой величины y и формируется управляющее воздействие, приближающее режим работы объекта к точке экстремума. Таким образом, система управления здесь имеет вид, подобный приведенному на рис. 1.9.

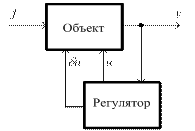
Рис. 1.9. Структура системы экстремального управления

Такие системы применяются для объектов, имеющих экстремальные характеристики и существенные, но медленно меняющиеся неконтролируемые факторы, приводящие к изменению экстремальных характеристик.

Системы оптимального управления решают задачу поддержания оптимальной по быстродействию работы системы регулирования при изменении режимов работы объекта. Структура подобной системы приведена на рис. 1.10.

Воздействие M изменяет параметры регулятора. Определение параметров регулирования производится на основе пробных изменений задающего воздействия .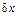

Рис 1.10. Структура системы оптимального управления

Объект вместе с регулятором можно рассматривать как систему, управляемую системой самонастройки. Параметры y и R, вводимые в систему самонастройки, являются управляемыми, а M − управляющим.

Поскольку система самонастройки выполняет двойное действие (управляет объектом и изучает его), то адаптивные системы являются устройствами дуального управления.

Развитие подобных систем активизировалось с развитием принципов построения надежных вычислительных устройств. Дуальное управление преследует двойную цель – изучение объекта и одновременное приведение его к требуемому режиму.

Классификация по типу сигнала. Понятия «переменная», «воздействие», «сигнал» в теории управления имеют информационный смысл: сигналы на входах и выходах являются носителями, а сами элементы – преобразователями (устройствами передачи и обработки) информации.

Если информация в системе кодируется уровнями сигналов-функций непрерывного времени (рис.1.11, а), то такая система называется непрерывной (аналоговой). В этом случае время и уровни сигналов принадлежат множествам мощности континуума.

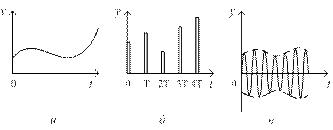
Рис. 1.11. Типы сигналов: непрерывные (а), дискретные (б),

с информационной огибающей (в)

Дискретные − это такие системы, в которых амплитуда входного сигнала может быть квантована по некоторому параметру. В зависимости от вида квантования различают дискретные по уровню (релейные), дискретные по времени (импульсные) и дискретные по уровню и времени (релейно-импульсные, цифровые)системы. Кроме того, в дискретных системах с обратной связью замыкание контура может происходить дискретно во времени.

Релейные – это системы, где в контуре регулирования стоит релейный элемент (реле), т.е. контур обратной связи замыкается тогда, когда ошибка d становится больше некоторой допустимой величины a (a – зона нечувствительности реле – заранее заданная величина),т.е. когда½ d ½³ a и размыкается, когда ошибка ½ δ ½£ b (отключение реле), где a > b. Отсюда следует, что в релейных системах производится квантование по уровню d ₀ (рис. 1.12, а), при котором в произвольные моменты времени выделяются значения непрерывного сигнала, достигшие одного из допустимых дискретных уровней. Отметим, что релейные системы существенно нелинейны и их нельзя заменять линейными математическими моделями. Отметим, что для построения систем оптимальных по быстродействию (важный класс систем управления!) в большинстве случаев используют системы с релейными элементами.

В импульсных системах производится квантование сигнала по времени, при котором в дискретные моменты времени выделяются значения непрерывного сигнала (рис. 1.12, б). Эти моменты отстоят друг от друга на постоянную величину Т, называемую шагом квантования.

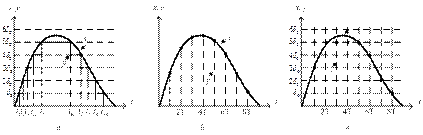
Рис 1.12. Квантование сигнала: а – по уровню, б – по времени,

в – по уровню и по времени

В релейно-импульсных системах производится одновременно квантование по уровню и дискретизация по времени, т.е. в равноотстоящие моменты времени непрерывный сигнал заменяется одним из фиксированных (допустимых) дискретных значений (рис. 1.12, в).

Существуют также дискретные системы, в которых информация кодируется частотой импульсов.

Область применения дискретных систем в настоящее время весьма разнообразна. Их подразделяют на две основные категории:

1. Системы, дискретные по своей природе, в которых существенная информация измеряется только в дискретные моменты времени. Примерами таких систем являются, например, радиолокационные системы обнаружения и сопровождения цели. Существует большое количество физических, биологических явлений, а также социальных и экономических процессов, которые могут быть описаны только дискретными моделями.

2. Системы, в которых непрерывная информация намеренно квантуется для получения новых, по сравнению с непрерывными системами, свойств (упрощение реализации, повышение надежности, увеличение точности и т.д.). Это системы, в состав которых входят компоненты вычислительной техники, в первую очередь микропроцессоры.

Еще одной важной разновидностью систем управления являются системы, в которых информация кодируется амплитудой переменного тока, т.е. огибающей несущего сигнала (рис.1.11, в). Примерами таких систем являются автоматические следящие системы с двигателями переменного тока, системы с радиоканалами с амплитудной модуляцией и т.д.

Классификация по типу алгоритма. Алгоритм управления на основе информации об ошибке d (t) = y * − y реализуется регулятором Р (рис. 1.13).

Рис. 1.13. Система автоматического управления

Он носит название закона регулирования (управления). Различают законы управления и соответственно регуляторы:

− пропорциональный (П-закон и П-регулятор), имеющий очень простую логику: чем больше ошибка, тем сильнее воздействие на объект:

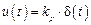, (1.1)

где k_P – коэффициент передачи регулятора, 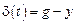– отклонение (ошибка) системы;

− интегральный (И-закон и И-регулятор), основанный на следующей идее: уровень воздействия на объект пропорционален суммарной ошибке, накопившейся за определенное время:

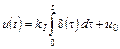, (1.2)

или

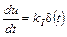, (1.3)

т.е. ошибка системы определяет скорость изменения управляющего воздействия, где 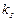– время изодрома (параметр настройки);

− пропорционально-интегральный (ПИ-закон и ПИ-регулятор) является комбинацией П- и И-законов:

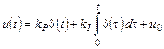; (1.4)

− дифференциальный (Д-закон и Д-регулятор),при котором величина воздействия определяется скоростью изменения ошибки:

,

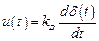где 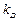– постоянная времени (параметр настройки);

− пропорционально-дифференциальный (ПД-закон), при котором управляющее воздействие определяется суммарным влиянием величины ошибки и скорости ее изменения:

;

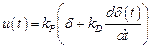− пропорционально-интегрально-дифференциальный (ПИД-закон и ПИД-регулятор), формирующий управляющее воздействие с учетом величины, суммарного текущего значения величины ошибки, ее накопления за определенное время и скорости изменения ошибки:

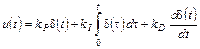. (1.5)

Классификация по энергетическому признаку. Исполнение принятого в управляющем устройстве решения об управляющем воздействии требует энергетических затрат, иногда весьма значительных.

Классификация по энергетическому признаку делит все системы управления на системы с регуляторами прямого и непрямого действия.

В системах прямого регулирования для оказания управляющего воздействия используется энергия самого управляющего процесса. В такой системе сигнал ошибки 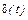должен быть достаточным по мощности для управления регулирующим органом. Примером такой системы может служить регулятор заданного уровня воды в паровом котле, изобретенный русским механиком И.И. Ползуновым в 1765 г. Применение подобной системы имело место в поплавковых регуляторах уровня топлива в карбюраторах автомобильных двигателей на заре отечественного автомобилестроения (рис. 1.14) и даже в современных мотоциклах.

Рис. 1.14. Регулятор прямого действия

Здесь поплавок одновременно выполняет три действия: измерение уровня, принятие решения об управляющем воздействии и исполнение решения. Английский механик Дж. Уатт построил систему прямого регулирования скорости вращения вала паровой машины на основе центробежного датчика скорости вращения.

Достоинством систем прямого регулирования является простота и надежность, недостатком – невысокая точность и необходимость больших усилий на перемещение управляющих органов (нужен большой поплавок, большая масса тел вращения центробежного регулятора и т.д.).

Для повышения точности управления объектами, требующими больших энергетических затрат на управление необходимо разделение функций элементов измерения и управления системы, а также привлечение дополнительного источника энергии. Эти два компонента отличают системы непрямого действия (рис. 1.15).

Измеритель-поплавок здесь имеет небольшие размеры, поскольку перемещение контакта потенциометра П не требует больших усилий. Напряжение d u, пропорциональное отклонению уровня от заданного, усиливается усилителем У и подается на двигатель Д. Последний перемещает через редуктор Р клапан на трубопроводе притока бензина.

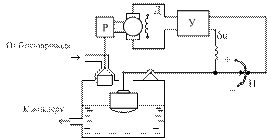
Рис. 1.15. Система регулирования непрямого действия

Достоинством систем непрямого действия является более высокая, чем у систем прямого действия, точность регулирования, недостатками – бóльшие сложность и стоимость, а также меньшая надежность.

Существуют и другие классификационные признаки. Среди них можно выделить:

1. Вид уравнений, описывающих систему. По этому признаку системы управления подразделяются на линейные и нелинейные. Линейных систем в природе нет, т.е. реально все существующие системы управления нелинейны. Поэтому под линейными системами понимаются приближенные линейные математические модели реальных нелинейных систем.

Большинство реальных систем можно свести к линейным, т.е. нелинейности в них являются несущественными (насыщение усилителей, петля гистерезиса и т.п.).

В тех случаях, когда нелинейности в системах управления существенны и их нельзя линеаризовать, рассматриваются нелинейные модели, и применяются методы исследования нелинейной теории автоматического управления.

2. Характер зависимости коэффициентов уравнений, описывающих систему от времени. По этому признаку системы управления бывают стационарными и нестационарными.

Стационарной называется система, реакция которой на любой тип возмущения не зависит от текущего состояния системы, а определяется лишь моментом времени воздействия возмущения. Например, математический или физический неизменяемый маятник, находящийся в покое, под воздействием возмущения заданной формы начнет совершать колебания, определяемые только параметрами сигнала возмущения, в какой бы момент времени это возмущение ни было бы приложено. Если реакция системы отсчитывается от некоторого момента времени t ₀, то реакция на возмущение x (t) представляет собой функцию y (t – t ₀). Точно также начало действия возмущения в момент времени t₁ = t₀ + a, т.е. в виде функции x (t – a) вызывает реакцию системы в виде функции y (t – t ₀ – a). Таким образом, в стационарной системе сдвиг во времени входного возмущения на некоторый интервал времени вызывает сдвиг реакции системы на тот же самый интервал. Такие системы описываются математическими (дифференциальными уравнениями) с постоянными коэффициентами.

В нестационарных системах при сдвиге входного возмущения во времени без изменения формы их выходные переменные не только сдвигаются по времени, но изменяют свою форму. Примером нестационарной системы может служить математический маятник, у которого длина нити меняется во времени по некоторому закону. При этом одно и то же входное возмущение с изменением длины нити будет вызывать разную реакцию системы.

3. Величина и характер ошибки 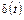. По этому признаку системы управления бывают статическими и астатическими.

В системах, статических по отношению к какому-либо воздействию, ошибка, вызванная этим воздействием, по окончанию процесса регулирования становится равной некоторой постоянной величине, называемой статической ошибкой.

В системах, астатических по отношению к какому-либо воздействию, ошибка, вызванная этим воздействием, по окончании процесса регулирования становится равной нулю.

4. Вид используемой энергии. В зависимости от вида используемой для управления энергии различают электрические, механические, гидравлические, пневматические, а также комбинированные системы автоматического управления.

Классы моделей. Общая классификация моделей систем управления приведена на рис. 1.16.

Четыре независимых признака дают возможность формирования 2⁴ = 16 типов непрерывных и дискретных моделей. Простейший класс – ЛСДК – линейные стационарные детерминированные конечномерные системы. Они описываются обыкновенными дифференциальными уравнениями с детерминированными коэффициентами. Для анализа и синтеза таких систем существует развитый математический аппарат. Далее мы будем рассматривать системы именно этого класса.

Более сложные классы формируются введением одного или нескольких альтернативных признаков. Для систем второго и более

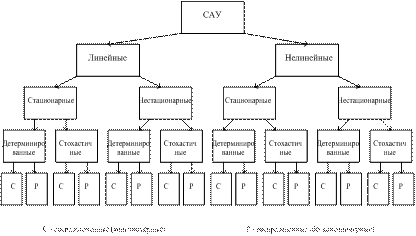
Рис. 1.16. Классификация систем автоматического управления

высоких уровней сложности анализ и синтез возможен только посредством вычислительных экспериментов.

Дата добавления: 2014-01-15