Понятие пространства состояний

В пространстве состояний

Средства описания моделей систем управления

Лекция 5

Современная теория автоматического управления оперирует с векторно-матричными моделями динамических систем. При этом рассматриваются в общем случае многомерные системы, т.е. системы произвольного порядка со многими входами и многими выходами, в связи с чем широко используются векторно-матричные уравнения и аппарат векторной алгебры.

Собственно система, ее входы и выходы − это три взаимосвязанных объекта, которые в каждой конкретной ситуации определяются соответственно математической моделью системы, заданием множеств входных и выходных переменных.

Для получения векторно-матричной модели (ВММ) исследуемая динамическая система представляется в виде “черного ящика” с некоторым числом входных и выходных каналов (рис. 2.21, а).

Рис. 2.21. Скалярное (а) и векторное (б) представления

динамической системы в виде "черного ящика"

Все переменные, характеризующие систему, можно разделить на три группы.

1. Входные переменные или входные воздействия, генерируемые системами, внешними по отношению к исследуемой системе. Они характеризуются вектором входа

,

где γ − число входов.

2. Выходные переменные, характеризующие реакцию системы на указанные входные воздействия. Представляются вектором выхода

,

где m − число выходов.

3. Промежуточные переменные, характеризующие внутреннее состояние системы, иначе − переменные состояния, представляются вектором

,

где n − число переменных состояния.

Состояние системы − это множество значений промежуточных переменных в данный момент времени. Новое состояние отличается от предыдущего значением хотя бы одной премежуточной переменной. Другими словами состояние – это та минимальная информация о прошлом, которая необходима для полного описания будущего поведения (т.е. выходов) системы, если поведение ее входов известно.

Совокупность входов можно рассматривать как один обобщенный вход, на который воздействует вектор входа U, совокупность выходов как вектор Y, а совокупность промежуточных координат, характеризующих состояние системы, − как вектор состояния X (см. рис. 2.21, б).

Решение задач анализа и синтеза связано с исследованием состояний системы, множество которых образует пространство состояний, .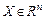

Исследование в пространстве состояний – это определение выходной реакции системы (совокупности значений выходных сигналов) для любой из допустимых совокупностей значений входных сигналов (вектора входа) и сигналов (векторов) состояния системы.

Дифференциальные уравнения в форме пространства состояний – это матричная форма записи системы дифференциальных уравнений, адаптированная для теории управления путем выделения из формы Коши алгебраических уравнений, связывающих внутренние координаты системы управления с выходной(ыми).

Дата добавления: 2014-01-15