Временные характеристики в форме

пространства состояний

Преобразовав по Лапласу систему дифференциальных уравне-

ний системы управления (2.14), получим систему операторных уравнений

и выражение для изображения вектора состояния

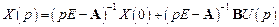. (2.28)

Первое слагаемое (2.28) определяет свободное движение системы, а второе – ее вынужденное движение.

Для получения оригинала (т.е. функции времени) необходимо выполнить обратное преобразование Лапласа. Оригинал скалярной функции с изображением

имеет, как нам уже известно, вид экспоненты

.

В матричном случае его аналог

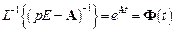
является матричной экспонентой, называемой матрицей перехода.

Произведению изображений соответствует свертка оригиналов, поэтому вектор состояния как функция времени получается из (2.28) в виде

.

Изображение переменной выхода при нулевых начальных

условиях определяется подстановкой второго слагаемого (2.28) во второе уравнение системы (2.26), т.е. в :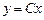

. (2.28, а)

При подаче на вход системы единичного импульса (U (p) = 1) реакция системы (импульсная переходная функция) выглядит так:

. (2.29)

Сравнивая последнее выражение с выражением для передаточной функции (2.27), видим, что

.

Следовательно, матрицу перехода можно получать путем обращения по Лапласу матрицы .

Пример 2.12. Пусть имеем матрицу состояний нормальной формы

.

Характеристическая матрица запишется как

,

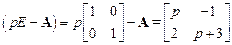а ее обращение есть

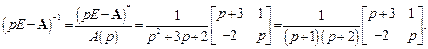
Применение обратного преобразования Лапласа к каждому элементу полученной матрицы приводит к получению матрицы перехода

.

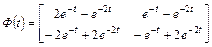Отсюда по формуле (2.29) при известных матрицах входа B = [0 1]^т и выхода C = [2 0] находится функция веса

Дата добавления: 2014-01-15