Лекция 9. Рис. 3.27. Амплитудно-фазовая характеристика звена чистого

А б

Рис. 3.27. Амплитудно-фазовая характеристика звена чистого

запаздывания: а − в комплексной плоскости, б − в действительном

пространстве

Окружность пересекает вещественную ось в точке +1 при 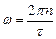и в точке −1 при .

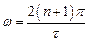Фазовая частотная характеристика равна

.

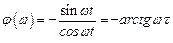Логарифмическая частотная характеристика есть

.

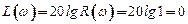Логарифмические частотная и фазовая характеристики приведены на рис. 3.28.

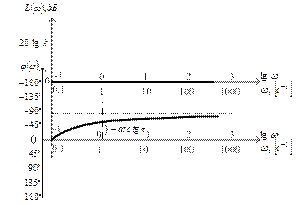
Рис.3.28. Логарифмические частотная и фазовая характеристики

элементарного звена чистого запаздывания

Таким образом, звено чистого запаздывания не изменяет амплитуду сигнала, а лишь вносит фазовый сдвиг, тем больший, чем больше время запаздывания τ.

Реальный пример звена чистого запаздывания привести достаточно сложно по причине идеальности самого процесса запаздывания. Некоторым реальным подобием такого звена может служить трубопровод достаточно большой длины, по которому перекачивается газ. Изменение параметров потока (давления, скорости течения и т.п.) распространяется по нему не мгновенно, а в течение некоторого времени, которое может рассматриваться как время запаздывания.

Идеальные элементарные звенья первого порядка. К ним относятся идеальные дифференцирующее и интегрирующее звенья.

Идеальное элементарное дифференцирующее звено – звено, выходной сигнал которого пропорционален дифференциалу (скорости изменения) входного сигнала, т.е. реализующее Д-закон управления.

Дифференциальное уравнение звена имеет вид:

.

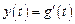Операторное представление дифференциального уравнения

.

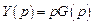Передаточная функция

.

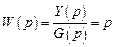Последнее выражение демонстрирует нереализуемость идеального дифференцирующего звена: в его передаточной функции порядок оператора числителя (1) выше порядка этого оператора в знаменателе (0). Физически это означает, что во временной области такое звено при наличии на входе ступенчатого единичного сигнала конечной мощности может обеспечить бесконечное возрастание амплитуды выходного сигнала за бесконечно малое время, а в частотной – возрастание усиления сигналов с увеличением частоты. И то и другое противоречит природе.

Условное графическое изображение идеального дифференцирующего звена приведено на рис. 3.29.

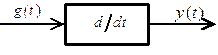
Рис 3.29. Условное графическое изображение

идеального дифференцирующего звена

Операторное изображение переходной функции есть

.

Оригинал переходной функции определяется как

.

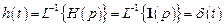Она представлена на рис. 3.30.

Рис.3.30. Переходная функция элементарного дифференцирующего звена

Импульсная переходная (весовая) функция определяется как

.

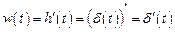Вид ее, при условии, что переходная функция (δ -функция Дирака) моделируется прямоугольным импульсом шириной τ, показан на рис. 3. 31.

Рис. 3.31. Весовая функция элементарного дифференцирующего звена

Частотная передаточная функция равна

,

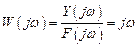при этом

,.

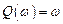Амплитудно-фазовая характеристика звена показана на рис. 3. 32.

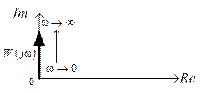
Рис. 3.32. Амплитудно-фазовая характеристика

элементарного дифференцирующего звена

Амплитудная частотная характеристика

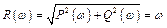
приведена на рис. 3.33.

Рис. 3.33. Амплитудная частотная характеристика

элементарного дифференцирующего звена

Фазовая частотная характеристика звена

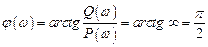
показана на рис. 3.34 (фазовый сдвиг имеет постоянное значение

на любой частоте).

Рис. 3.34. Фазовая частотная характеристика

элементарного дифференцирующего звена

Логарифмическая амплитудная характеристика определяется выражением

.

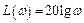Логарифмические амплитудная и фазовая частотные характеристики приведены на рис. 3.35.

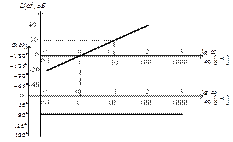
Рис. 3.35. Логарифмическая частотная характеристика

элементарного дифференцирующего звена

Наклон логарифмической амплитудной характеристики соответствует +20 дБ на декаду. Коэффициент усиления также увеличивается с частотой, что также указывает на его физическую нереализуемость.

Идеальное элементарное интегрирующее звено – звено, выходной сигнал которого пропорционален интегралу от входного сигнала

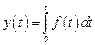(3.7.)

или

.

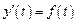Операторное представление дифференциального уравнения интегрирующего звена есть

.

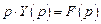Соответствующая ему передаточная функция определяется как

.

Условное графическое обозначение звена показано на рис. 3.36.

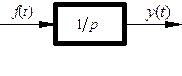
Рис. 3.36. Условнее графическое обозначение

элементарного интегрирующего звена

Операторное изображение переходнойфункции рассматриваемого звена

,

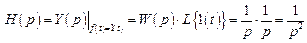а его оригинал имеет вид

.

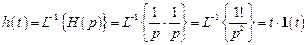Графическое представление переходной функции интегрирующего звена приведено на рис. 3.37.

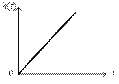
Рис. 3.37. Переходная функция элементарного интегрирующего звена

Импульсная переходная (весовая) функция определится как

.

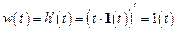Ее изображение приведено на рис. 3.38.

Рис. 3.38. Весовая функция элементарного интегрирующего звена

Частотная передаточная функция интегрирующего звена есть

,, .

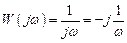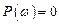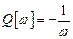Амплитудно-фазовая характеристика звена показана на рис. 3.39.

Рис. 3.39. Амплитудно-фазовая характеристика

элементарного интегрирующего звена

Амплитудная частотная характеристика звена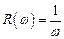

приведена на рис. 3.40.

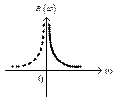
Рис. 3.40. Амплитудная частотная характеристика

элементарного интегрирующего звена

Фазовая частотная характеристика звена есть

.

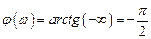Логарифмическая амплитудная характеристика определяется логарифмированием амплитудной частотной характеристики и имеет вид

.

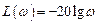Логарифмические амплитудная и фазовая частотные характеристики приведены на рис. 3.41.

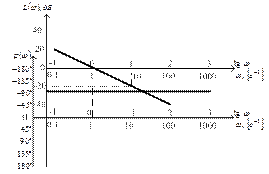
Рис. 3.41. Логарифмическая частотная характеристика

элементарного интегрирующего звена

Наклон логарифмической амплитудной характеристики соответствует –20 дБ на декаду, т.е. звено усиливает низкочастотные и ослабляет высокочастотные сигналы.

Дата добавления: 2014-01-15