Типовые звенья

Типовые звенья первого порядка. К ним относятся типовые:

– идеальное и реальное дифференцирующее звенья;

– идеальное и реальное интегрирующее звенья;

– апериодическое звено;

– форсирующее звено.

Типовые идеальные дифференцирующее и интегрирующее звенья отличаются от элементарных наличием множителя k, т.е. они являются последовательным соединением соответствующего элементарного звена и идеального усилительного звена, как показано рис. 3.42 и 3.43.

Рис. 3.42. Условное графическое изображение

типового идеального дифференцирующего звена

Рис. 3.43. Условное графическое изображение

типового идеального интегрирующего звена

Все полученные выше выражения характеристик соответствующих элементарных звеньев и графики функций будут, очевидно, справедливы для типовых одноименных звеньев, если их амплитудные характеристики умножить на коэффициент усиления усилительного (пропорционального) звена k. Временные характеристики типовых дифференцирующего и интегрирующего звеньев приведены в табл. 3.4.

Таблица 3.4

Временные характеристики

типовых дифференцирующего и интегрирующего звеньев

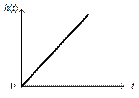
Наименование характеристики	Типовое дифференцирующее звено	Типовое интегрирующее звено
Переходная функция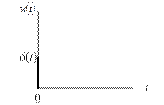
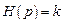
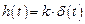
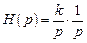
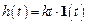
Весовая функция

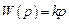
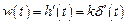
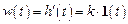
Рассмотрим частотные характеристики указанных звеньев.

1. Типовое дифференцирующее звено:

– частотная передаточная функция

;

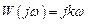– амплитудно-фазовая характеристика

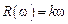
приведена на рис. 3.44.

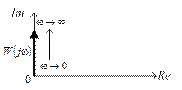
Рис. 3.44. Амплитудно-фазовая характеристика

типового дифференцирующего звена

Амплитудная и фазовая частотные характеристики совпадают с рис. 3.32 и 3.34 соответственно.

Логарифмическая амплитудная характеристика определяется выражением

.

Логарифмические амплитудная и фазовая частотные характеристики типового дифференцирующего звена приведены на рис. 3.45.

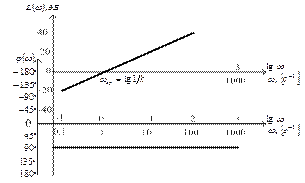
Рис. 3.45. Логарифмические амплитудная и фазовая

частотные характеристики типового дифференцирующего звена

– фазовая частотная характеристика

,

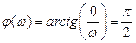а ее графическое представление совпадает с рис. 3.34.

Примером идеализированного дифференцирующего звена является RC -цепь при R = 0, показанная на рис 3.46.

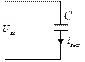
Рис. 3.46. Дифференцирующая цепь

Уравнение связи выхода с входом для этой цепи при нулевых начальных условиях есть

,

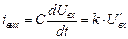т.е. совпадает по форме с (3.6).

2. Типовое идеальное интегрирующее звено:

– частотная передаточная функция

,

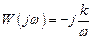– амплитудная частотная характеристика

,

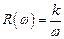а ее графическое изображение совпадает с рис 3.40.

Логарифмическая амплитудная частотная характеристика интегрирующего звена есть

.

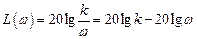Ее графическое представление приведено на рис. 3.47.

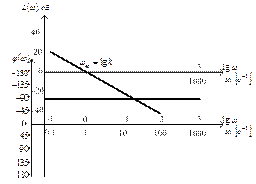
Рис. 3.47. Логарифмические частотная и фазовая характеристики

интегрирующего звена

Фазовая частотная характеристика описывается выражением

.

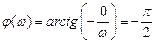Примером реализации идеального интегрирующего звена может служить RL -цепь при R = 0, показанная на рис. 3.48.

;

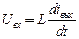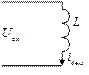
Рис. 3.48. Пример реализации интегрирующего звена

Для этой цепи при нулевых начальных условиях

,

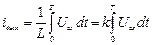где 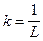(1/Гн) – коэффициент передачи. Как видно, последнее выражение по структуре совпадает с (3.7).

3. Апериодическое (инерционное) звено. Апериодическое (инерционное) звено– реальное инерционное звено, выходной сигнал которого пропорционален разности входного сигнала и накопившейся энергии выходного сигнала.

Дифференциальное уравнение, описывающее это звено, выглядит так

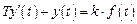, (3.8)

где k – коэффициент передачи (усиления), T – постоянная времени (инерционности), измеряемая в секундах.

Выражение для передаточной функции может быть получено на основе представления структурной операторной схемы апериодического звена с помощью элементарных звеньев. Представим уравнение (3.8) в виде

,

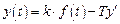или в операторной форме

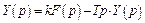. (3.9)

Выражению (3.9) соответствует операторная схема, приведенная на рис. 3.49.

Рассматривая схему на рис. 3.49 как одноконтурную систему управления с обратной связью, получим передаточную функцию апериодического звена как передаточную функцию такой системы. Для этого отмечаем, что:

– передаточная функция прямого пути равна ;

– передаточная функция пути обратной связи есть .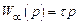

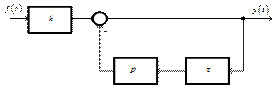
Рис. 3.49. Операторная структурная схема апериодического звена

Тогда передаточная функция замкнутой системы есть

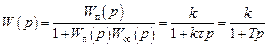. (3.10)

Выше было отмечено, что временные характеристики соединения звеньев с обратной связью удобнее получать с помощью обратного преобразования Лапласа эквивалентной передаточной функции. Операторное изображение переходной функции апериодического звена, полученное на основе выражения (3.10), имеет вид

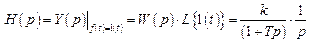. (3.11)

Оригинал переходной функции из (3.11) есть

.

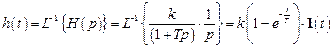Переходная функция апериодического звена приведена на рис. 3.50.

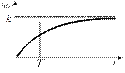
Рис. 3.50. Переходная функция апериодического звена

Из рис. 3.50 следует, что с уменьшением T переходной процесс будет заканчиваться быстрее.

Импульсная переходная (весовая) функция есть производная переходной функции:

.

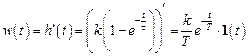Вид этой функции иллюстрируется рис. 3.51.

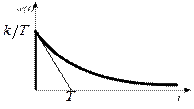
Рис. 3.51. Импульсная переходная функция апериодического звена

Частотная передаточная функция соединения звена

.

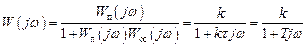Представление передаточной функции апериодического звена в виде суммы вещественной и мнимой частей есть

.

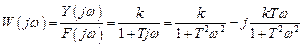Напомним, что разделение передаточной функции на вещественную и мнимую части производится умножением числителя и знаменателя на число, комплексно-сопряженное знаменателю, в данном случае на .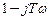

Действительная частотная характеристика для апериодического звена есть

,

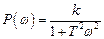а мнимая частотная характеристика есть

.

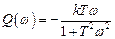График частотной характеристики апериодического звена в обычном масштабе приведен на рис. 3.52. Она представляет собой полуокружность радиуса k /2.

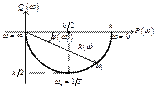
Рис. 3.52. Амплитудно-фазовая характеристика

апериодического звена

Амплитудная частотная характеристика апериодического звена имеет вид

.

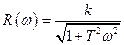Она приведена на рис. 3.53.

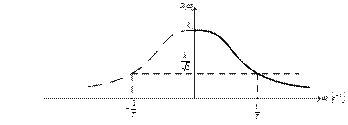
Рис. 3.53. Амплитудная частотная характеристика

апериодического звена

Фазовая частотная характеристика апериодического звена выражается следующим образом:

.

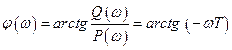Логарифмическая амплитудная частотная характеристика определяется выражением

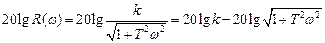
или

.

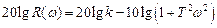Построение асимптотической логарифмической амплитудной характеристики производится на основе следующего анализа.

1. При малых частотах, где 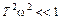, вторым слагаемым пренебрегаем (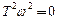), поэтому

.

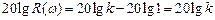2. При больших частотах, где 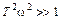, пренебрегаем первым слагаемым, тогда

.

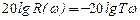3. В области средних частот 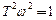, отсюда определяем частоту сопряжения низкочастотной и высокочастотной составляющей (собственную частоту апериодического звена):

,

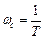где 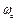- собственная частота апериодического звена.

Теперь построим логарифмическую фазовую частотную характеристику. Из выражения

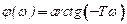
следует, что 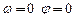при , при 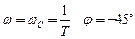, а при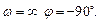

Расчетные логарифмическая амплитудная и фазовая частотные характеристики при 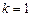приведены на рис. 3.54.

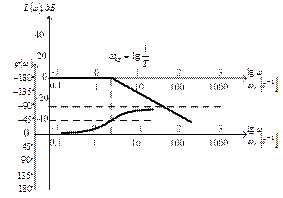
Рис. 3.54. Логарифмические амплитудная и фазовая характеристики

апериодического звена

При 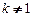амплитудная характеристика перемещается параллельно самой себе по оси ординат на величину 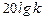, а фазовая – остается той же самой (коэффициент усиления 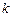не входит в выражение фазовой характеристики).

Действительная амплитудная частотная характеристика, как известно из практики, отличается от асимптотической не более, чем на 3 дБ на частоте сопряжения (что допустимо для инженерных расчетов).

Примером реализации апериодического звена может служить RL -цепь, изображенная на рис. 3.55.

Уравнение функционирования схемы

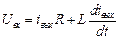
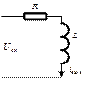
Рис. 3.55. Пример апериодического звена

Поделив на R, получим

,

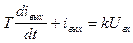где 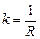, [1/Ом] – коэффициент передачи апериодического звена, 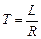, [ с ] − постоянная времени апериодического звена.

Другими примерами апериодического звена могут быть:

– генератор постоянного тока, входной величиной которого является напряжение на обмотке возбуждения, а выходной – напряжение на якоре;

– резервуар с газом, у которого входной величиной является величина давления на вводе в него, а выходной – давление в резервуаре;

– нагревательная печь с входной величиной – количеством поступающего в нее тепла и выходной – температурой в печи.

4. Форсирующее звено. Выходной сигнал форсирующего звена представляет собой сумму, одно слагаемое которой пропорционально входному сигналу, а другое – скорости его изменения. Характеристики форсирующего звена обратны характеристикам апериодического звена.

Его дифференциальное уравнение из (3.2) имеет вид

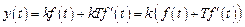, (3.11)

где T – постоянная времени форсирующего звена.

Операторное представление дифференциального уравнения

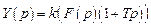. (3.12)

Выражениям (3.11) или (3.12) соответствует операторная схема, приведенная на рис. 3.56.

Рис. 3.56. Операторная структурная схема форсирующего звена

Передаточная функция параллельного соединения звеньев, как было показано выше, равна сумме передаточных функций звеньев. Поэтому передаточная функция форсирующего звена равна

.

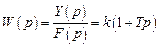Из последнего выражения видно, что передаточная функция форсирующего звена представляет собой сумму передаточных функций пропорционального и дифференцирующего звеньев.

Временные характеристики параллельного соединения также определяются суммой временных характеристик звеньев. Операторное изображение переходной функции есть

.

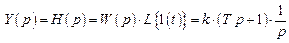Оригинал переходной функции есть обратное преобразование Лапласа ее операторного представления

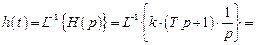
Из последнего выражения видно, что переходная функция форсирующего звена представляет собой сумму переходных функций элементарного усилительного звена и последовательного соединения звеньев дифференцирующего звена и звена чистого запаздывания, что полностью соответствует рис. 3.58.

Импульсная переходная (весовая) функция есть производная переходной функции

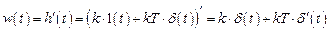
и представляет собой сумму весовых характеристик элементарного усилительного звена и последовательного соединения звеньев дифференцирующего звена и звена чистого запаздывания, что также полностью соответствует рис. 3.58.

Очевидно, что временные функции форсирующего звена представляют собой приподнятые на величину k одноименные характеристики элементарного дифференцирующего звена.

Частотная передаточная функция форсирующего звена есть

.

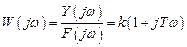Вещественная и мнимая частотные передаточные функции параллельного соединения звеньев определяются как суммы соответствующих характеристик звеньев. Для усилительного звена

,

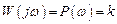а для последовательного соединения элементарных дифференцирующего звена и звена запаздывания

.

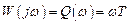Амплитудная частотная характеристика определяется выражением

,

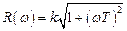а фазовая частотная характеристики есть

.

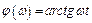Логарифмическая амплитудная частотная характеристика форсирующегозвена определяется как

.

Отсюда следует, что при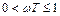

,

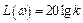а при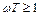

.

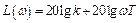Эти соотношения отражены на графиках логарифмических характеристик форсирующего звена, приведенных на рис. 3.57.

Дата добавления: 2014-01-15