Лекция 13. Пусть передаточная функция разомкнутой системы равна

Пусть передаточная функция разомкнутой системы равна

,

где и – полиномы степеней m и n соответственно, тогда передаточная функция замкнутой системы может быть представлена в виде

.

Характеристический полином замкнутой системы можно представить в виде суммы и вначале построить годографы и , а затем и сложить их графически. Если (коэффициент усиления системы), то годограф получается из годографа путем смещения его вправо вдоль вещественной оси на величину k.

Пример 4.6. Определить предельный коэффициент усиления системы с передаточной функцией в разомкнутом состоянии

,

состоящей из трех инерционных звеньев.

Решение. Характеристическое уравнение замкнутой системы есть

.

Для решения задачи необходимо построить годограф Михайлова. Поскольку , построим сначала годограф разомкнутой системы

,

где

(4.12)

Он показан на рис. 4.12.

Для получения годографа замкнутой системыдостаточно сместить мнимую ось влево на величину k. При k = k_пред система будет на границе устойчивости (годограф пройдет через начало координат). Величина k_пред может быть определена из си-

Рис. 4.12. Годограф системы

стемы уравнений

(4.13)

где – частота, соответствующая точке пересечения годографас действительной осью. Из уравнений (4.12) и (4.13) получим

;

.

■

Критерий Найквиста также основан на анализе частотных характеристик и удовлетворение этому критерию является необходимым и достаточным условием устойчивости систем с обратной связью. Он оценивает устойчивость замкнутой системы по характеристикам разомкнутой системы.

Рассмотрим одноконтурную систему с передаточной функцией разомкнутого контура 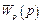. Рациональная функция

называется возвратной разностью и представляет собой определитель одноконтурного сигнального графа с отрицательной обратной связью.

Легко увидеть, что

, (4.14)

т.е. возвратная разность равна отношению характеристических полиномов замкнутой и разомкнутой систем. Нулями являются корни характеристического полинома замкнутой системы, а полюсами – корни характеристического полинома разомкнутой системы .

Пусть C – произвольный замкнутый контур без самопересечений на p -плоскости p, а – рациональная функция аргумента p, не имеющая на контуре C ни нулей, ни полюсов. Разность между количеством нулей и полюсов функции , заключенных внутри замкнутой кривой C, равна числу полных оборотов вектора вокруг начала координат, в то время как точка p обходит контур C по часовой стрелке. В качестве контура C, как и ранее, выбирается мнимая ось и правая полуокружность бесконечного радиуса.

Ранее было установлено, что если разомкнутая система устойчива, то изменение аргумента ее характеристического полинома равно

. (4.15)

Тогда замкнутая система сохранит устойчивость, если

,

или с учетом (4.14)

. (4.16)

Последнее тождество будет иметь место, если кривая при движении вдоль контура C по часовой стрелке не будет охватывать начала координат p-плоскости, т.е. точки (0, j 0), как показано на рис. 4.13.

Переместив мнимую ось на единицу вправо, получим следующую формулировку критерия Найквиста для случая устойчивой разомкнутой системы:

Рис. 4.13. Годограф замкнутой системы

Для устойчивости замкнутой системы необходимо и достаточно, чтобы амплитудно-фазовая характеристика (годограф) разомкнутой системы при движении p вдоль C по часовой стрелке не охватывала точку (– 1, j 0).

На рис. 4.14, а показан случай устойчивой замкнутой системы, которая устойчива в разомкнутом состоянии.

Рис. 4.14. Иллюстрация критерия Найквиста

Если годограф проходит через критическую точку (–1, j 0) на частоте , то пара корней характеристического полинома замкнутой системы окажется чисто мнимой 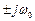. Этот случай называется колебательной границей устойчивости (рис. 4.14, б).

Из предыдущего рассмотрения видно, что рациональные функциии имеют одни и те же полюсы.

Если среди них имеется l правых, т.е. разомкнутая система не-

устойчива, то для нее применение принципа аргумента (4.15) выражается так:

,

а тождество (4.16) приобретает вид

.

В силу симметричности характеристик:

можно ограничиться рассмотрением только случая 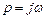, , т.е. половины контура C на комплексной плоскости и записать последнее тождество в виде

,

и сформулировать критерий Найквиста для случая неустойчивой

разомкнутой системы следующим образом:

Для устойчивости замкнутой системы необходимо и достаточно, чтобы амплитудно-фазовая характеристика разомкнутой системы охватывала точку (– 1, j 0 ) раз против часовой стрелки, где l – число правых корней характеристического полинома (правых полюсов передаточной функции) разомкнутой системы.

Пример 4.7. Пусть передаточная функция разомкнутой системы есть

,

т.е. имеет один правый полюс (разомкнутая система неустойчива). Для устойчивости замкнутой системы АФХ при изменении ω от нуля до ∞ должна ½ раза охватить точку (–1, j 0) против часовой стрелки (рис. 4.15).

Рис. 4.15. Пример применения критерия Найквиста

Из рис. 4.15 видно, что это возможно при k > 1 (замкнутая система устойчива при k = k ₁ и неустойчива при k = k ₂). Для перемещения корня из правой полуплоскости в левую необходимо достаточно большое усиление контура.

■

Для систем высокого порядка амплитудно-фазовая характеристика может иметь сложный вид, затрудняющий подсчет числа охватов критической точки. В этом случае для упрощения рекомендуется считать число переходов АФП через луч (–∞, –1) (переход снизу вверх – отрицательный, сверху вниз – положительный). Для устойчивости замкнутой системы необходимо и достаточно, чтобы сумма переходов равнялась бы + p /2, где p – число правых полюсов передаточной функции разомкнутой системы. Особенно удобно применение критерия Найквиста, если строятся логарифмические частотные характеристики:

.

Если передаточная функция разомкнутой системы имеет p правых полюсов, то для устойчивости замкнутой системы необходимо и достаточно, чтобы в интервале частот, где L_p > 0, число переходов через линию −p равнялось бы p /2 (переход снизу вверх – положительный, сверху вниз – отрицательный).

Критерий Найквиста – физичен: здесь хорошо видна роль амплитудных и фазовых преобразований, вносимых контуром, на устойчивость системы в целом. Изначальный смысл применения критерия Найквиста состоит в выявлении роли контура в перемещении корней характеристического полинома системы. По этому критерию можно судить о влиянии свойств элементов на характер свободных движений системы в целом.

Практически важным является также возможность исследования устойчивости систем с обратными связями на основе экспериментально снятых частотных характеристик звеньев, образующих контур.

Устойчивость систем, описываемых переменными состояния. Если система представлена сигнальным графом в переменных состояния, то определитель этого графа совпадает с характеристическим полиномом, к которому можно применить известные критерии устойчивости.

Однако модель может быть задана совокупностью дифференциальных уравнений относительно переменных состояния. В этом случае удобно изобразить альтернативную модель в виде сигнального графа, по которому легко записать его определитель , а, значит, и характеристическое уравнение.

Пример 4.8. Пусть система описывается двумя дифференциальными уравнениями первого порядка:

,

,

где – входной сигнал.

Соответствующая этой системе уравнений модель приведена на рис. 4.16.

Рис. 4.16. Сигнальный граф

Граф содержит три контура: , и , причем ине имеют общего узла. Тогда, согласно правилу Мейсона, определитель графа есть

.

Умножив на p ², получим характеристическое уравнение

.

Поскольку для устойчивости системы все коэффициенты урав-

нения должны быть положительны, то требование по устойчивости может быть представлено в виде условия .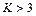

■

Суть рассмотренного метода получения характеристического уравнения непосредственно по векторному дифференциальному уравнению

(4.16)

состоит в том, что поскольку решение такого уравнения представляет собой экспоненту, то можно найти такие , при которых решение для каждой переменной состояния будет иметь вид

,

при этом

.

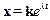Подставив последнее выражение в (4.16), получим

или

,

откуда следует система однородных уравнений

,

где E – единичная матрица, а 0 – нулевая матрица. Нетривиальное решение этой системы существует, только если обращается в нуль определитель матрицы , т.е. если

.

Раскрывая определитель, получаем уравнение n -го порядка, которое и является характеристическим уравнением системы.

Устойчивость систем с типовой структурой. Рассмотрим системы, образованные соединениями типовых звеньев, и определение их асимптотической устойчивости по начальному состоянию.

Системы без контуров. Характеристический полином параллельного и последовательного соединений звеньев равен произведению характеристических полиномов звеньев

.

Отсюда следует, что необходимым и достаточным условием устойчивости параллельного и последовательного соединений звеньев является устойчивость каждого из звеньев, составляющих систему.

Одноконтурные системы. Характеристический полином системы, образованной встречно-параллельным соединением звеньев, есть

.

Если система имеет в прямом и обратном пути некоторые (произвольные) множества звеньев с передаточными функциями

,

то характеристический полином записывается в виде суммы

(4.17)

полиномов числителя

и знаменателя

передаточной функции разомкнутой системы

.

В общем случае без предварительных вычислений о расположении корней полинома (4.17) ничего сказать нельзя. Поэтому необходимо вычислить корни либо применить некоторый критерий устойчивости.

Однако есть два практически важных случая, когда информа-

цию о расположении корней можно получить при минимуме вычислений.

1. Если полиномы и имеют нетривиальный общий делитель – полином , т.е. передаточная функция разомкнутой системы W_р имеет диполи, то при замыкании системы соответствующие корни характеристического полинома не перемещаются, поскольку из выражения

следует, что корниявляются также и корнями . Таким образом, для устойчивости системы с обратной связью необходимо выполнение условия: все корни полинома

левые. Отсюда следует также условие неустойчивости: наличие у полиномови общего делителя с правым корнем.

Как было показано выше, наличие общих корней у полиномов числителя и знаменателя передаточной функции соответствует неполной системе. При замыкании неполная часть своих свойств не изменяет.

2. Если при обходе аргументом p замкнутого контура С выполняется условие

(4.18)

или при изменении частоты в интервале от 0 до ∞

, (4.19)

то характеристический полином замкнутой системы имеет в правой полуплоскости столько же корней, что и характеристический полином разомкнутой системы , т.е. если разомкнутая система устойчива, то замкнутая система также будет устойчивой.

Выберем в качестве замкнутой кривой C кривую, образованную мнимой осью и правой относительно нее полуокружностью бесконечного радиуса (контур Найквиста), показанную на рис. 4.17.

Рис. 4.17. Контур Найквиста

Из (4.18), (4.19) следует, что для устойчивости замкнутой системы, устойчивой в разомкнутом состоянии, достаточно, чтобы

,

т.е. чтобы амплитудно-фазовая характеристика разомкнутой системы принадлежала единичному кругу с центром в начале координат (рис. 4.18).

Рис. 4.18. Амплитудно-фазовая характеристика

Запасы устойчивости. Изменение параметров систем управления (в частности, коэффициентов усиления и запаздываний) в процессе их эксплуатации может вызвать их неустойчивость. Поэтому при проектировании систем необходимо обеспечить гарантированную устойчивость систем при изменении параметров в некоторых пределах. Такое проектирование базируется на понятиях запасов устойчивости систем управления, вводимых на основе критерия Найквиста.

Запасы устойчивости характеризуют удаление частотного годографа (годографа Найквиста) разомкнутой системы от критической точки с координатами (–1, j 0). Если амплитудно-частотная характеристика на частоте проходит через точку (–1, j 0), то характеристический полином имеет пару мнимых корнейи система будет неустойчивой. Если годограф проходит на некотором удалении от критической точки, то система будет иметь некоторый запас устойчивости.

Для количественной оценки удаленности годографа от точки (–1, j 0), а, значит, и левых корней полинома от мнимой оси, используется понятие запаса устойчивости по модулю (амплитуде) и запаса устойчивости по фазе.

Запас устойчивости по модулю (усилению) есть отношение предельного коэффициента усиления системы к коэффициенту усиления в исследуемом состоянии. Он показывает, насколько можно увеличить модуль амплитудно-фазовой характеристики разомкнутой системы без потери устойчивости замкнутой системы.

Типовая амплитудно-фазовая характеристика устойчивой по

модулю разомкнутой системы, которая будет устойчивой и после замыкания контура, приведена на рис. 4.19, а.

Рис. 4.19. К оценке запаса устойчивости по годографу разомкнутой системы: а – по модулю, б – по фазе

Запас устойчивости по модулю β определяется как отношение

,

где – частота пересечения годографа разомкнутой системы с вещественной осью.

Согласно критерию Найквиста это отношение обратно пропорционально отрезку 0А (см. рис. 4.19, а) на отрицательной действительной полуоси

,

где – частота, на которой фазовый сдвиг, вносимый контуром, равен –π радиан. Для устойчивых систем β > 1, для систем на границе устойчивости β = 1 (= –1). Обычно β = 2…10.

Запас устойчивости по фазе (рис. 4.19, б) определяется как

,

где – частота среза, на которой модуль амплитудно-фазовой

характеристики разомкнутого контура равен 1. Он измеряется по дуге окружности единичного радиуса с центром в начале координат между точкой с координатами (–1, j 0) и ближайшей к ней точкой частотного годографа. Частота пересечения годографа есть частота среза , на этой частоте . Для неустойчивой системы запас по фазе считается отрицательным. Запас устойчивости по фазе обычно составляет величину .

Запасы устойчивости удобно изображать в логарифмическом масштабе, как показано на рис. 4.20.

При этом запас по модулю определяется как

,

а б

Рис. 4.20. Запасы устойчивости по модулю и фазе, определяемые по логарифмическим частотным характеристикам:

а – устойчивая система, б – неустойчивая система

а запас по фазе определяется на частоте, на которой . Величины и положительны для устойчивых систем и отрицательны – для неустойчивых систем.

Частота среза также является косвенным показателем качества процессов. Она приближенно равна мнимой части доминирующих комплексных корней (частоте колебаний процессов). Если предположить, что за время регулирования в системе имеет место 1…2 колебания, то

.

Дата добавления: 2014-01-15