Лекция 15

А б

Инвариантность (робастность) систем управления

Лекция 14

Понятие инвариантности. Под инвариантностью систем управления понимается независимость некоторых ее переменных от воздействий. Требования по инвариантности могут быть различными для различных переменных системы. Так управляемая переменная 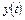в общем случае зависит как от задающего 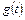, так и от возмущающего 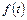воздействий. Поэтому для нормального функционирования системы она должна быть инвариантной (нечувствительной, не обладающей реакцией) к возмущению и ковариантной (адекватной по реакции) с задающим воздействием.

Математическая трактовка понятия инвариантности системы управления состоит в следующем. Пусть на систему действует входное (задающее g (t) или возмущающее f (t)) воздействие, которое обозначим символом ψ (t) и ошибка управления 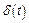описывается дифференциальным уравнением

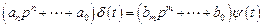. (4.20)

Решение этого уравнения состоит из переходной составляющей 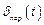, определяемой общим решением уравнения (4.20) без правой части, и вынужденной составляющей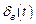, определяемой частным решением уравнения (4.20) с правой частью.

Изображение ошибки при нулевых начальных условиях можно описать как

,

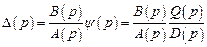где 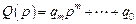, 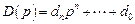– некоторые полиномы.

В соответствии с теоремой о разложении оригинал ошибки может быть представлен в виде

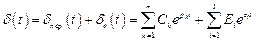, (4.21)

где p_k – полюсы передаточной функции, т.е. корни уравнения 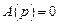, а z_i – полюсы входного воздействия, т.е. корни уравнения .

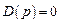Вынужденная составляющая 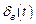будет тождественно равна нулю в следующих случаях:

1. 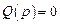(входное воздействие равно нулю). Это – тривиальный случай и интереса не представляет.

2. 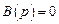(система абсолютно инвариантна к входному воздействию ψ (t), которое может быть произвольной функцией времени). Это условие означает, что равна нулю передаточная функция системы по ошибке 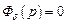, либо равна единице передаточная функция замкнутой системы 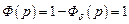. Последнее предполагает бесконечную полосу пропускания системы независимо от частоты. В реальных системах это невозможно, т.е. реализация абсолютной инвариантности сталкивается с принципиальными трудностями.

3. Равенство 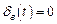имеет место для воздействий, изображения которых имеют все полюсы (корни уравнения 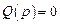), совпадающие с нулями передаточной функции (корнями уравнения 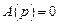). В этом случае после разложения полиномов 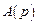и 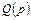на множители 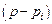общие множители можно сократить, при этом второе слагаемое (4.21) обращается в нуль и .

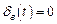Последний случай носит название случая частичной инвариантности, т.е. инвариантности к входным воздействиям определенного вида.

Формы инвариантности. При оценке инвариантности систем управления используются следующие формы инвариантности:

– абсолютная инвариантность, при которой должно выполняться условие равенства нулю передаточной функции по возмущающему воздействию для всех значений комплексного аргумента

,

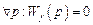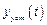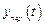при этом оказываются равными нулю составляющие и вынужденного движения системы;

– избирательная абсолютная инвариантность, определяемая как условие равенства нулю передаточной функции системы на полюсах p_k изображения возмущения

;

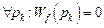– инвариантность с точностью до ε, при которой для передаточной функции по возмущающему воздействию должно выполняться условие

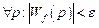
для всех значений комплексного аргумента, т.е. когда требуется не тождественность 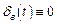, а приближенное равенство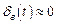, мерой выполнения которого является величина ε, в этом случае вынужденные составляющие движений системы оказываются ограниченными, а сама форма инвариантности называется избирательной (селективной);

– избирательная инвариантность до ε (ограниченность установившейся реакции системы на воздействие того или иного типа) достигается при

;

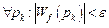при этом следует стремиться минимизировать значение модуля

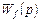в той области комплексной плоскости, где размещаются полюсы изображения воздействия, поскольку малость значений передаточной функции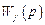

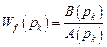, k =1, 2,…, n_F

означает малость установившихся составляющих реакции;

– инвариантность к входным воздействиям определенного вида, при которых имеет место равенство нулю вынужденной составляющей ошибки .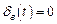

Важным условием инвариантности является отсутствие резонанса в системе, т.е. совпадения полюсов изображения воздействия с полюсами передаточной функции системы (комплексных частот воздействия с собственными комплексными частотами p_k = p_i). Как следует из описания реакции системы на произвольное воздействие

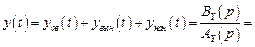
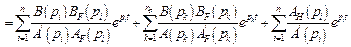, (4.22)

для уменьшения вероятности уменьшения резонанса следует отдалять полюсы передаточной функции от полюсов воздействия (это увеличивает значения характеристического полинома передаточной функции воздействия 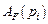) и приближать нули передаточной функции к полюсам воздействия (это уменьшает ).

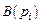Точно также абсолютная ковариантность управляемой переменной с задающим воздействием достигается при

.

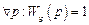Из (4.22) следует, что система хорошо воспроизводит задающее воздействие, если передаточная функция 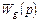имеет близкие значения на полюсах воздействия

.

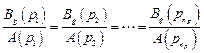Это значит, что амплитудно-частотная характеристика системы по каналу воспроизведения должна быть постоянной на всем спектре задающего сигнала. На рис. 4.21, а приведены графики амплитудно-частотных характеристик абсолютно инвариантной (1) и инвариантной до ε (2) системы, а на рис. 4.21, б – абсолютно ковариантной (1) и ковариантной до ε (2), где M – показатель колебательности системы.

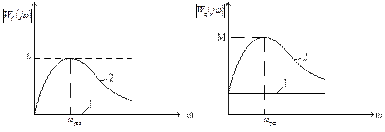
Рис. 4.21. АЧХ инвариантной (а) и ковариантной (б) систем

Проведенные выше обсуждения инвариантности предполагают, что система асимптотически устойчива, т.е. свободная 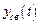и переходная 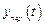составляющие со временем затухают до 0, т.е.

.

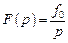Избирательная инвариантность к степенным воздействиям. Наиболее часто обеспечивается избирательная инвариантность к постоянному воздействию, имеющему нулевой полюс. Установившаяся вынужденная составляющая 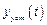реакции системы определяется выражением

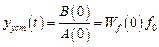. (4.23)

Чем меньше статический коэффициент усиления системы по возмущающему воздействию, тем меньше установившееся значение отклонения управляемой переменной и тем в большей степени достигается избирательная инвариантность до ε. Если передаточная функция имеет нулевой нуль

,

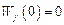то имеет место нулевая установившаяся реакция на постоянное воздействие, т.е. избирательная абсолютная инвариантность. Система, обладающая таким свойством, называется астатической.

Если воздействие имеет двукратный нулевой полюс

,

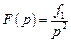то для определения вынужденной установившейся составляющей вместо (4.23) следует воспользоваться более общим выражением (4.21). Проще, однако, воспользоваться теоремой о конечном значении оригинала

.

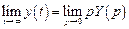Для рассматриваемого случая

.

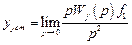Если передаточная функция системы имеет нулевой нуль

,

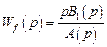то установившееся отклонение выходной величины от возмущения, изменяющегося с постоянной скоростью, равно постоянной величине

.

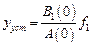Для абсолютной избирательной инвариантности в этом случае система должна иметь двукратный нулевой нуль, т.е. иметь астатизм второго порядка.

Теперь рассмотрим общий случай степенного воздействия

,

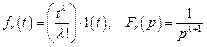где λ = 1, 2, … – показатель степенного воздействия (при λ = 1 имеем единичное степенное воздействие).

Изображение этого воздействия имеет λ + 1-кратный нулевой полюс. Если передаточная функция системы имеет ν-кратный нулевой нуль, то

.

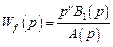Тогда предельное значение реакции системы на степенное воздействие

.

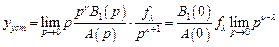Отсюда следует, что при ν > λ в системе имеет место нулевая установившаяся реакция, при ν = λ установившаяся реакция постоянна, а при ν < λ установившаяся реакция на возмущение имеет бесконечное значение, т.е. в этом случае система управления неработоспособна.

Избирательная инвариантность к гармоническому воздействию. Пусть к системе приложено гармоническое возмущение

,

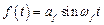изображение которого

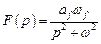
имеет чисто мнимые полюсы .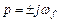

Установившаяся реакция на гармоническое возмущение является также гармонической с той же частотой 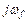, но с другой амплитудой и фазой

,

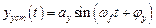где

;

.

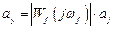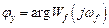Если модуль комплексной частотной характеристики по каналу возмущения мал, то имеет место селективная инвариантность до ε. Для абсолютной избирательной инвариантности переменной выхода полином числителя 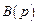передаточной функции 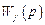должен иметь сомножитель 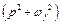, т.е. пару мнимых корней .

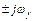Инвариантность систем с типовой структурой. Инвариантность систем с типовой структурой обеспечивается различно в зависимости от структуры системы управления, т.е. от реализуемых принципов управления.

Последовательная компенсация воздействия. Обеспечение абсолютной инвариантности переменной выхода при последовательной компенсации возмущения (рис. 4.23) может быть обеспечено,

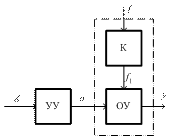
Рис. 4.23. Последовательная компенсация возмущений

если выполняется условие

,

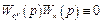где 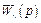, 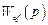– передаточные функции компенсатора и объекта по каналу возмущения соответственно.

Инвариантность до ε достигается, если

,

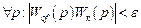а абсолютная инвариантность к воздействию с полюсами изображения 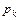имеет место при

.

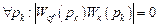Это означает, что передаточная функция компенсатора (или объекта) должна иметь нули, равные полюсам возмущения. Так, при

постоянном возмущении

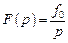
условие абсолютной инвариантности сводится к наличию у передаточной функции 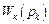нулевого нуля. Это обеспечивает нулевую установившуюся реакцию объекта при любом уровне 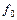постоянного воздействия. Если сам объект имеет по каналу возмущения интегрирующие свойства, т.е. передаточная функция 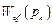имеет нулевой полюс, то передаточная функция 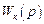должна иметь двукратный нулевой нуль.

Хотя последовательная компенсация выглядит весьма привлекательно, ее реализация связана с изменением конструкции самого объекта или технологии управляемого процесса (например, защита от электромагнитных полей требует применения экранирования).

Для достижения ковариантности управляемой переменной 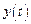с задающим воздействием 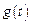управляющее устройство соеди-

няют последовательно с объектом, как показано на рис. 4.23.

Рис. 4.23. Обеспечение ковариантности

Выполнение условий абсолютной ковариантности

,

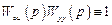ограничивается возможностью физической реализуемости устройства управления. В связи с инерционностью объекта степень полинома знаменателя его передаточной функции по каналу управления 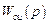должна быть выше полинома числителя, поэтому по первому условию абсолютной ковариантности передаточная функция 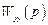должна иметь степень числителя выше степени знаменателя. Тем не менее абсолютная ковариантность вполне реализуема, так как первое условие абсолютной ковариантности должно выполняться только на полюсах задающего воздействия, т.е при p = p_k, k = 1, 2,…, n_G. Например, при наличии постоянных уровней в сигнале задания (на выходе – установившийся режим)

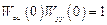
и установившееся значение переменной выхода будет в точности равно заданию. Необходимо только, чтобы коэффициент усиления устройства управления был равен величине, обратно пропорциональной коэффициенту усиления объекта по каналу управления.

Параллельная компенсация воздействия. Она является эффективным средством обеспечения инвариантности объекта к основному возмущению, если это возмущение может быть измерено. Ее

реализация показана на рис. 4.24.

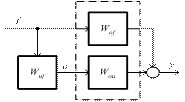
Рис. 4.24. Параллельная компенсация возмущения

Условие ее достижения может быть записано в виде

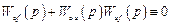
или

.

Поскольку

; ,

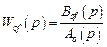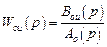то передаточная функция по каналу возмущения есть

.

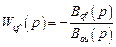Во многих практических случаях инерционные свойства объекта по обоим каналам примерно совпадают, поэтому передаточная функция устройства управления оказывается физически реализуемой.

При наличии не менее двух каналов передачи воздействия f условия абсолютной инвариантности являются реализуемыми (принцип двухканальности Б.Н. Петрова). При этом подразумевается, что передаточная функция одного из каналов выбрана надлежащим образом. В рассматриваемом случае – это передаточная функция параллельной компенсации 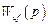, реализуемой в устройстве управления.

Более простые реализации условия инвариантности обеспечивают избирательную инвариантность. Если, например, возмущение имеет постоянную величину, то установившаяся реакция объекта равна нулю при

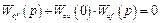
или

.

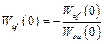При этом передаточная функция системы от входа f до выхода y будет иметь нулевой нуль без включения дифференцирующего звена, как этого требует последовательная компенсация.

Компенсация воздействий в системах с обратной связью. Механизм действия возмущений в системах с обратной связью ил-

люстрируется рис. 4.25.

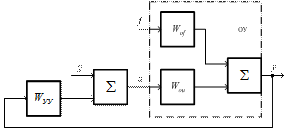
Рис. 4.25. Реализация принципа обратной связи

Передаточная функция системы от входа f к выходу y есть

.

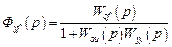Абсолютная инвариантность управляемой переменной достига-

ется при тождественности нулю передаточной функции системы. Пр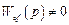и и 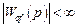, она обеспечивается при бесконечном усилении контура на всех частотах

.

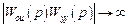Как известно, повышение усиления контура вызывает проблему устойчивости замкнутой системы, т.е. одним повышением усиления обеспечить инвариантность системы с обратной связью не удается. При конечном усилении в системе с отрицательной обратной связью можно ослабить влияние возмущения на выход системы. Можно сказать, что устойчивые системы с обратной связью при достаточно большом усилении контура инвариантны к возмущениям до ε.

Избирательная инвариантность к возмущениям со спектром { p_k } имеет место, если передаточная функция замкнутой системы обращается в нуль также на спектре возмущений.

Для нахождения условий селективной инвариантности необходимо определить вид передаточных функций канала управления (для упрощения записи опустим комплексную переменную p)

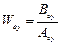
и управляющего устройства

,

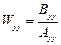при которых эти условия обеспечиваются. Запишем выражение передаточной функции в виде отношения полиномов. Пусть передаточные функции объекта по обоим каналам имеют одинаковые знаменатели, т.е.

,

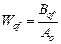тогда

.

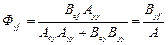Если передаточные функции по каналам управления и возмущения не имеют нулей и полюсов, общих с нулями и полюсами изображения возмущения, то из последнего выражения следует, что для селективной инвариантности системы передаточная функция устройства управления должна иметь полюсы, равные полюсам изображения возмущения. Если возмущение постоянно, т.е. его изображение имеет нулевой полюс, то полином управления должен иметь значение 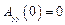, т.е. должен содержать интегрирующее звено. О такой структуре говорят, что она обладает астатизмом. При отсутствии интегратора в такой системе можно достичь только избирательной инвариантности до ε, т.е. в системе будет иметь место статическая ошибка.

При степенном воздействии (его изображение имеет много-

кратный нулевой полюс) для абсолютной избирательной инвариантности управляющее устройство должно иметь нулевые полюсы той же кратности. Если же кратность полюса передаточной функции будет на единицу меньше кратности полюса возмущения, то будет иметь место избирательная инвариантность до ε (ненулевая установившаяся ошибка).

При гармоническом воздействии известной частоты 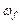амплитуда установившихся колебаний будет равна нулю, если передаточная функция управления имеет мнимые полюсы , т.е. управляющее устройство должно содержать консервативное звено.

Таким образом, передаточная функция управляющего устройства должна иметь полюсы, равные полюсам возмущения (т.е. быть «похожей» на изображение возмущения). Этот факт является выражением принципа внутренней модели: в хорошей системе должна присутствовать модель среды.

В абсолютно инвариантной системе нулевая установившаяся ошибка сохраняется при любом воздействии и при любом изменении ряда параметров системы, т.е. абсолютная инвариантность является астатичной. Это достигается за счет бесконечного усиления контура на комплексных частотах возмущения. При конечном усилении имеет место селективная инвариантность до ε. Для этого должно выполняться условие

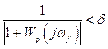
или (поскольку )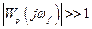

,

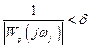или

.

Это значит, что на частоте возмущения усиление контура должно быть достаточно большим. При использовании логарифмического масштаба это условие принимает вид

.

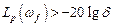При необходимости ослабить амплитуду возмущения в сто раз (δ = 0.01) усиление контура на частоте возмущения должно быть равно

.

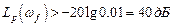Основным методом построения инвариантных систем является применение комбинированного управления, когда наряду с регулированием по отклонению (по ошибке) используется регулирование по задающему или возмущающему воздействию. Структурная схема такой системы приведена на рис. 4.26.

При отсутствии регулирования по задающему воздействию, т.е. при 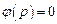, регулируемая величина y связана с задающим воз-

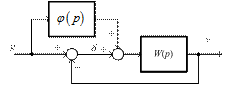
Рис. 4.26. Структура системы с комбинированным управлением

действием g через передаточную функцию замкнутой системы:

,

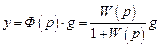где 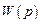– передаточная функция разомкнутой системы.

При введении регулирования по задающему воздействию регулируемая величина определяется выражением

.

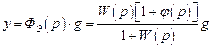Отсюда эквивалентная (с учетом регулирования по задающему воздействию) передаточная функция по ошибке

,

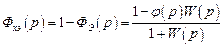а следующее из последнего выражения условие полной инвариантности системы имеет вид .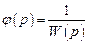

Разложив последнее выражение в ряд по степеням p, получим вид функции, определяющей вводимый сигнал от управляющего воздействия

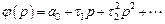, (4.24)

где a ₀ – безразмерное число.

Таким образом, для получения полной инвариантности в управляющий сигнал необходимо вводить его первую и высшие производные. Обычно точность их введения уменьшается с возрастанием порядка производной (путем использования дифференцирующих звеньев). Поэтому практически можно получить лишь частичную инвариантность, что соответствует введению ограниченного числа членов разложения (4.24).

Дата добавления: 2014-01-15