Лекция 18

5.4. Частотный метод синтеза

Постановка задачи. Этот метод активно развивался, начиная с 50-х годов. Он применяется, в основном, как графический и не позволяет получить точных оценок показателей качества, но является достаточно простым методом синтеза. Метод применяется, в основном, для синтеза линейных скалярных систем и иногда эффективно применяется для расчета нелинейных систем.

Для данного метода необходимо:

- задать математическую модель объекта в виде передаточных функций и от них перейти к частотным характеристикам;

- построить по заданным показателям качества желаемые частотные характеристики;

- определить структуру корректирующего звена регулятора с помощью передаточных функций или частотных характеристик.

Будем рассматривать объект управления (рис. 5.5), поведение которого описывает передаточная функция W_O(p), а выходная переменная измеряется с помехой H (t). Влияние окружающей среды отражает возмущение f (t).

Рис. 5.5. Расчетная структурная схема системы

Требования к поведению замкнутой системы заданы в виде оценок переходного процесса, в качестве которых используются статическая ошибка (δ_* ), перерегулирование (σ_*) и быстродействие (t^*_p).

Необходимо определить передаточную функцию W_к(p) регулятора (корректирующего звена), включение которого в систему обеспечит в ней заданное качество работы.

Частотный метод синтеза предполагает использование асимптотических логарифмических амплитудных частотных характеристик, он применяется для расчета одноканальных систем, функционирующих в режиме слежения или отработки входного воздействия. Предполагается, что корректирующее звено (регулятор) находится на входе системы.

Рассмотрим в начале реакцию системы только на входное воздействие g, полагая возмущение и помеху измерения равными нулю (f=0, H =0), их влияние мы учтем в дальнейшем. Определим сначала передаточную функцию разомкнутой системы

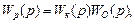(5.27)

а затем замкнутой

(5.28)

Как видим, передаточную функцию замкнутой системы однозначно определяет W_p(p).

Таким образом, если удастся сформировать определенную передаточную функцию или частотную характеристику для разомкнутой системы, то тем самым можно обеспечить требуемые свойства замкнутой системе.

Влияние частотной характеристики разомкнутой системы на свойства замкнутой. Рассмотрим подробнее связь между частотными характеристиками разомкнутой и замкнутой систем, для чего перейдем от передаточной функции (5.27) к частотной характеристике

(5.29)

Исследуем характеристику (5.29) в различных областях частот как это принято в инженерной практике. Введем предварительно несколько определений.

Областью низких частот будем называть область изменения ω вблизи нуля. В ней по условию статики выполняется соотношение

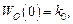
где k_о коэффициент усиления объекта. Обычно k_о >>1, поэтому для

разомкнутой системы в соответствии с (5.29) получим

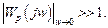(5.30)

Областью высоких частот будем называть совокупность частот, намного превышающих полосу пропускания системы. Здесь справедливы соотношения

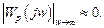(5.31)

Под зоной средних частот будем понимать промежуток между зонами низких и высоких частот, где выполняются соотношения

(5.32)

Поскольку частотные характеристики разомкнутой и замкнутой систем связаны соотношением, аналогичным (5.28), с учетом (5.30) в области низких частот получим

т.е. частотная характеристика разомкнутой системы практически не влияет на аналогичную характеристику замкнутой системы.

В области высоких частот с учетом (5.31) справедливо соотношение

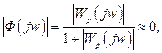
а, следовательно, частотная характеристика разомкнутой системы также не влияет на свойства замкнутой.

Таким образом, наибольшее влияние разомкнутая система окажет на свойства замкнутой в области средних частот, где необходимо наиболее тщательно формировать частотную характеристику W(jω).

Основные соотношения частотного метода синтеза. На основе выражения (5.29) получим расчетные соотношения частотного метода синтеза. Если удается задать определенную частотную характеристику разомкнутой системы W_p^*(jω), то из (5.29) можно вычислить W_k(jω). Однако этот способ является громоздким и не нашел практического применения, но на его основе разработан удобный метод синтеза по ЛАЧХ. Запишем его расчетное соотношение, для чего частотную характеристику разомкнутой системы представим в форме

В соответствии с (5.29) для амплитудных частотных характеристик справедливо равенство

которое в логарифмическом масштабе принимает вид

(5.33)

Поскольку в результате расчета реальная амплитудная частотная характеристика должна совпасть с желаемой, то приравнивая правую часть (5.33) ,получим

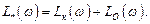
Отсюда следует расчетное соотношение для логарифмической характеристики регулятора, которое является основным в частотной методе синтеза

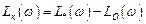. (5.34)

Таким образом, для расчета регулятора необходимо построить логарифмическую амплитудную частотную характеристику объекта и на основе требований к качеству процессов в замкнутой системе сформировать логарифмическую амплитудную частотную характеристику разомкнутой системы. Затем следует определить логарифмическую амплитудную частотную характеристику регулятора в соответствии с выражением (5.34).

Построение асимптотической логарифмической амплитудной частотной характеристики объекта. Часто модель объекта управления представляет собой последовательную цепочку типовых звеньев, поэтому L_о (ω) можно получить, суммируя отдельные логарифмические амплитудные частотные характеристики. Подобное суммирование позволяет предложить следующую процедуру построения L₀ (ω).

- на частоте ω = 1 (или в логарифмическом масштабе 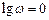) фиксируется точка, соответствующая значению , где k _О – коэффициент усиления объекта;

- на оси абсцисс отмечаются частоты сопряжения (или ), , 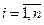где п – число типовых звеньев в составе передаточной функции объекта;

- до первой частоты сопряжения строится низкочастотная асимптота с наклоном –20 r дБ/дек, если W_о(p) содержит интегрирующие звенья, а r – число таких звеньев. Наклон характеристики будет равен +20 l дБ/дек, если передаточная функция объекта содержит дифференцирующие звенья, l - число этих звеньев. Низкочастотная асимптота строится таким образом, чтобы она сама или ее продолжение проходили через точку ;

- на частотах сопряжения происходит «излом» асимптотической логарифмической амплитудной частотной характеристикиобъекта. Наклон ее изменяется на -20 r дБ/дек, если соответствующая частоте сопряжения постоянная времени находится в знаменателе передаточной функции объекта, r - число таких звеньев. «Излом» асимптотической логарифмической амплитудной частотной характеристики будет равен +20 l дБ/дек, если постоянная времени находится в числителе передаточной функции, l - число звеньев. Новая асимптота проводится до следующей частоты сопряжения, где также происходит ее «излом» в соответствии с указанным правилом.

Для построения ЛАЧХ объекта с произвольной передаточной функцией

следует перейти к выражению для частотной характеристики

Амплитудная частотная характеристика определяется так:

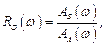
что позволяет вычислить

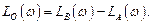(5.35)

Таким образом, логарифмическая амплитудная частотная характеристика объекта находится как разность (5.35).

Построение желаемой логарифмической амплитудной частотной характеристики. Поскольку желаемая логарифмическая амплитудная частотная характеристика строится на основе требований к качеству работы замкнутой системы в статике и динамике, рассмотрим эти режимы отдельно.

Так как в основном статическую ошибку в системе (см. рис. 5.10) порождает возмущающее воздействие (см. разд. 4), то

необходимо обеспечить выполнение условия

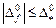, (5.36)

где

есть величина максимально допустимой статической ошибки; 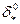- ее относительное значение; - действительная статическая ошибка системы от возмущения.

Известно, что на величину статической ошибки влияет общий коэффициент усиления , который равен произведению коэффициентов усиления объекта и регулятора .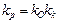

В случае статической системы ошибка соответствует выражению (5.15), т.е.

С учетом требования (5.36) расчетное соотношение для k _р принимает вид

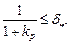(5.37)

Для астатических систем, работающих в режиме линейной заводки, коэффициент усиления k_р можно определить на основе выражения (4.30, б)

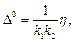
где 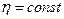представляет собой допустимое значение коэффициента ошибки.

При синтезе систем частотным методом удобно «выровнять» по коэффициенту ЛАЧХ объекта и строить ЛАЧХ разомкнутой системы с коэффициентом усиления k_р. Таким образом, требование по статике учитывается на этапе построения логарифмической характеристики объекта.

Обсудим теперь построение желаемой ЛАЧХ разомкнутой системы, которую будем выбирать из условий требуемой динамики замкнутой системы. Так как наибольшее влияние на свойства замкнутой системы разомкнутая оказывает в области средних частот (см. п. 5.4.2), построение желаемой характеристики начинается именно в этой области частот (рис. 5.6).

Рис. 5.6. Среднечастотная асимптота желаемой ЛАЧХ

Опытным путем установлено, что для обеспечения заданных динамических свойств наклон среднечастотной асимптоты следует выбирать равным -20 дБ/дек., причем ось абсцисс она пересекает в точке lg ω _ср. Частота среза ω _ср в данном методе играет роль граничной частоты полосы пропускания, при этом значение АЧХ системы становится равным единице.

Частота ω _ср выбирается по заданному быстродействию и перерегулированию замкнутой системы, а соотношение между t^*_р и ω _ср устанавливают номограммы, приводимые в справочной литературе. Для предварительных расчетов можно пользоваться выражением

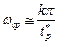, (5.38)

где k = (2...4) и зависит от величины заданного перерегулирования.

Длина среднечастотного участка желаемой L (ω) логарифмической амплитудной характеристики ограничивается запасом устойчивости по модулю ΔL, который откладывается вверх и вниз по оси ординат. В свою очередь, ΔL находится по номограммам (рис. 5.11) в зависимости от требуемого перерегулирования σ*. Приближенно длина среднечастотного участка l = (1... 1,5) декады, причем вправо и влево от lg ω _ср длина асимптоты составляет 0,5 l. В этом случае в системе будет обеспечено перерегулирование σ = (20...30) %.

Далее переходим к построению желаемой характеристики в области высоких и низких частот. Поскольку L_о(ω) строится с учетом рассчитанного из условий статики коэффициента усиления к_р, для обеспечения требуемой статической ошибки следует обеспечить совпадение в области низких частот L *(ω) с логарифмической амплитудной характеристикой объекта. В области высоких частот эти две характеристики могут совпадать или быть параллельными. Далее среднечастотная часть сопрягается с низкочастотной и высокочастотной асимптотами желаемой логарифмической амплитудной характеристики. Наклон логарифмической амплитудной характеристики на участках сопряжения должен быть кратным ±20 дБ/дек, их следует проводить так, чтобы получить наиболее простую характеристику.

Пример 5.2. Построить асимптотическую логарифмическую амплитудную характеристику объекта, передаточная функция которого имеет вид

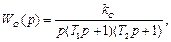
где коэффициент усиления k_O = 10, а постоянные времени T₁ = 10 с, T₂ = 1 с.

Решение. Предварительно представим передаточную функцию в виде

откуда следует, что система представляет собой последовательное соединение усилительного, интегрирующего и двух апериодических звеньев.

Определим характерные точки (точки излома асимптотической логарифмической амплитудной характеристики):

дБ;

дек.;

и отметим их на осях координат (рис. 5.7).

Рис. 5.7. Асимптотическая ЛАЧХ объекта для примера 5.2

Логарифмическая амплитудная характеристика начинается из области низких частот, которая расположена левее первой частоты сопряжения. Низкочастотная асимптота имеет наклон –20 дБ/дек, так как передаточная функция объекта содержит интегрирующее звено. Проводится она до частоты lg ω ₁ так, чтобы ее продолжение пересекало ось ординат в точке 20 lg k _о. На частоте lg ω ₁ происходит «излом» характеристики на -20 дБ/дек., что соответствует первому апериодическому звену в составе W_О(p). Следовательно, до следующей частоты сопряжения (lg ω ₂) асимптота имеет наклон -40 дБ/дек. «Излом» характеристики на частоте lg ω ₂ равен –20 дБ/дек., так как в составе W_О(p) есть второе апериодическое звено с постоянной времени Т₂, так что наклон последней асимптоты ЛАЧХ объекта будет равен –60 дБ/дек.

■

Определение передаточной функции регулятора. Асимптоти-

ческую логарифмическую амплитудную характеристику регулятора определим графически в соответствии с основным соотношением частотного метода синтеза (5.34) в виде

.

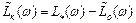По найденной характеристике определим частоты сопряжения, где происходит излом L_о(ω), и соответствующие им значения постоянных времени. Передаточная функция W_к(р) определяется на основе процедуры, обратной по отношению к правилу построения логарифмической амплитудной характеристики объекта. Причем в окончательную передаточную функцию регулятора следует добавить коэффициент усиления k_к = k_р/k_О, рассчитанный по условиям статики, т. е.

.

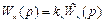Реализовать полученную передаточную функцию можно на пассивных или активных элементах. При этом следует учитывать, что переход от передаточной функции к структурным звеньям возможен посредством сигнальных графов в формах с фазовой переменной либо с многомерным входом и последующим переходом к структурным графам. Отметим также, что в этом методе синтеза для реализации регулятора можно использовать любой из вариантов структурных схем.

■

Пример 5.6. Для системы с передаточной функцией объекта

и построенной по заданным требованиям к динамике и статике логарифмической характеристикой L_*(ω) (рис. 5.8) необходимо определить передаточную функцию регулятора.

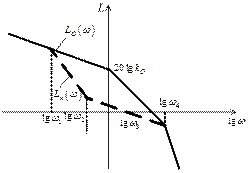
Рис. 5.8. Иллюстрация частотного метода синтеза

Предварительно графически найдем L_к(ω) как разность между желаемой характеристикой L_*(ω) системы и ЛАЧХ объекта L_о(ω). Определим частоты сопряжения ω_i, i = 1÷4, которые соответствуют точкам излома характеристики корректирующего звена L_к(ω) и запишем передаточную функцию регулятора в ви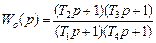де

, где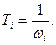

Схематично полученную передаточную функцию можно представить в виде цепочки последовательно соединенных интеграторов с прямыми и обратными связями. Такое представление позволяет легко перейти к реализации корректирующего звена на активных элементах.

■

Влияние возмущения и помехи измерения на свойства замкнутой системы. Обсудим теперь влияние возмущения и помехозащищенность системы, рассчитанной частотным методом, для чего вернемся к ее исходной структуре (см. рис. 5.5).

Рассмотрим сначала случай, когда помеха измерения пренебрежимо мала (H = 0). Запишем выражение для выходной переменной системы

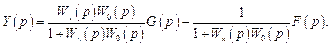(5.39)

В соответствии с постановкой задачи синтеза необходимо, чтобы выходная переменная повторяла входной сигнал 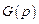независимо от влияния возмущения . Обсудим, как система справляется с этой задачей, для чего исследуем ее поведение на различных частотах.

В области низких частот в соответствии с (5.30), т.е. , справедливо условие | W _k(jω) W ₀(jω)|>>1, поэтому вторая составляющая выражения (5.39) при замене p на jω обращается в нуль, а y ≈ g. Таким образом, система на низких частотах достаточно хорошо выполняет свою функцию.

Вблизи частоты среза (в области средних частот) согласно (6.32), т.е. , справедливо соотношение 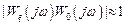, а составляющие входа следующие: y = 0,5 g и y_f = 0,5 f. Очевидно, что в такой ситуации система плохо воспроизводит вход и плохо подавляет возмущение, т. е. работает «частично».

В области высоких частот в соответствии с (6.31), т.е. 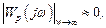для частотных характеристик справедливо соотношение | W _к(jω) W ₀(jω)|<<1,поэтому вместо выражения (6.39)получим y_g ~ 0и y_f ~ f.Как видим, в этом случае система также не справляется с поставленной задачей.

Следовательно, чем шире полоса пропускания (чем больше ω_ср) тем лучше в условиях действия возмущений система выполняет свое назначение. При построении желаемой логарифмической характеристики разомкнутой системы необходимо учитывать этот факт и стремиться по возможности увеличивать ω_ср.

Обсудим теперь влияние помехи Н,полагая входное воздействие g и возмущение fравными нулю. Поскольку объект, как правило, имеет ограниченную полосу пропускания и в этом случае выступает в роли фильтра, то высокочастотная помеха не будет проходить на выход системы. В основном помеха оказывает влияние на управляющее воздействие, для которого операторное выражение имеет вид

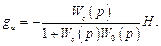(5.40)

Рассмотрим соответствующую частотную характеристику и запишем приближенные выражения для управления (5.40) на различных частотах.

В области низких частот, когда | W_k (jω) W ₀(jω)|>>1, получим

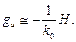
Как видим, влияние помехи будет тем меньше, чем больше коэффициент усиления объекта.

Для области средних частот справедливо условие | W_k(jω)W₀(jω) | ≈1, при этом

т. е. влияние помехи повышается по сравнению с предыдущим случаем.

В области высоких частот при выполнении соотношения (5.31) составляющую управления, порожденную помехой, приближенно можно оценить следующим образом:

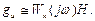
Таким образом, в этом случае влияние помехи полностью определяется свойствами корректирующего звена.

Следовательно, для уменьшения влияния помехи на низких и средних частотах нужно применять «качественный» датчик, а на высоких частотах помеху измерения H(t) можно парировать путем использования регулятора, обладающего интегрирующими свойствами. Подобный эффект будет наблюдаться, если степень полинома числителя передаточной функции W_к (p) меньше степени полинома ее знаменателя. В случае когда степени полиномов А_к(р) и В_к(р) равны, в регулятор рекомендуется добавить апериодическое звено с малой постоянной времени.

Процедура синтеза регулятора частотным методом. Обобщая рассмотренные этапы частотного метода синтеза, можно предложить следующую процедуру расчета регулятора.

1. Определяется коэффициент усиления разомкнутой системы k_р из условия заданной статической ошибки по соотношению (5.36), а затем вычисляется коэффициент усиления регулятора (корректирующего звена) k_к =k_p/k₀.

2. Строится асимптотическая логарифмическая амплитудная частотная характеристика объекта с учетом рассчитанного коэффициента усиления регулятора k_к, т. е. .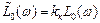

3. На основании требований к качеству процессов в замкнутой системе ( и σ^*) формируется желаемая логарифмическая амплитудная частотная характеристика разомкнутой системы .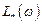

4. Графически вычисляется логарифмическая амплитудная частотная характеристика регулятора согласно соотношению

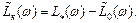
5. На основе 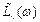восстанавливается передаточная функция W_к(p),а затем записывается передаточная функция регулятора W_к(р)= k_к(р .

6. Анализируется влияние возмущения f(t) и в случае необходимости увеличивается частота среза ω _ср, для которой повторяются пп. 3-5 процедуры расчета регулятора.

7. С целью уменьшения влияния помехи измерения к рассчитанной передаточной функции W_к(р) корректирующего звена добавляется передаточная функция апериодического звена с малой постоянной времени.

8. Предлагается схемная реализация регулятора на активных или пассивных элементах.

Пример 5.7. Для следящей системы управления одним из звеньев руки робота из примера 5.2 (рис. 5.9) рассчитать регулятор, который обеспечивал бы следующее качество процессов: время установления t_n < 2 с, перерегулирование σ < 30 %, скоростная ошибка δ_ск < 2,5 %.

Рис. 5.9. Структурная схема системы управления

одним из звеньев руки робота

Решение. Здесь

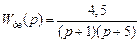
и

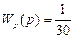
есть передаточные функции двигателя и редуктора,

есть передаточная функция регулятора, который включает в себя корректирующее звено W_к(р) и усилитель мощности с передаточной функцией

При расчете W_k(р) коэффициент усиления усилителя мощности k_УМ добавим к передаточной функции объекта, т. е. будем рассматривать

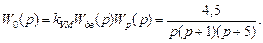
В соответствии с процедурой синтеза определим коэффициент усиления корректирующего звена из условия заданной скоростной ошибки (см. пример 5.2):

С учетом численных значений получим 1/0,9k_к < 0,025 и

k > 45. Выберем отсюда k_к = 50.

Для построения асимптотической логарифмической амплитудной частотной характеристики запишем в виде

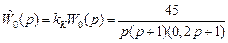
и определим следующие характерные точки:

дБ; 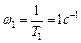,, дек.

Асимптотическая ЛАЧХ приведена на рис. 5.10.

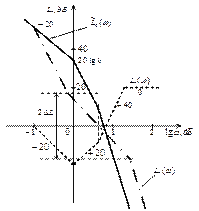
Рис. 5.10. Логарифмические АЧХ к примеру 5.7

Построим теперь желаемую ЛАЧХ, среднечастотный участок

которой имеет наклон -20 дБ/дек. Исходя из заданного перерегулирования σ* < 30 %, по номограммам [2] (рис. 5.11) определим

Рис. 5.11. Номограммы для определения параметров желаемой ЛАЧХ

Р_mах = 1,22

и

ω_н = 4π/t_n* = 6,5 с^-1.

Частоту среза обычно находят по соотношению

ω_ср = (0.6...0.9)ω _н,

поэтому выберем

ω _ср = 5с^–1.

В этом случае

lg ω _ср = 0,7 дек.

Запас устойчивости по модулю, ограничивающий среднечастотный участок логарифмической амплитудной частотной характеристики, также определим по номограмме, ΔL = 16дБ. В результате получим, которая приведена на рис. 5.10.

Определим теперь и запишем

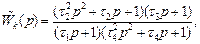
где 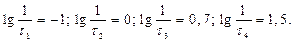Отсюда следует, что 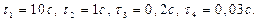Окончательно запишем

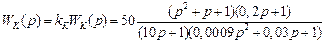
или

.

Схемная реализация полученной передаточной функции корректирующего звена, соответствующая второму каноническому представлению (сигнальному графу в форме с фазовой переменной), приведена на рис. 5.12.

Рис. 5.12. Пример схемной реализации регулятора

5.5. Модальный метод синтеза

Основные понятия. Модальный метод синтеза обычно применяется для расчета систем, работающих в режиме отработки начальных условий. Поскольку процедура расчета основана на использовании корней характеристического уравнения, которые относятся к модальным характеристикам системы, метод синтеза получил название «модального».

Рассмотрим основные соотношения метода для случая, когда математическая модель объекта управления представлена в переменных состояния

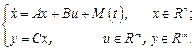(5.41)

Требования к поведению замкнутой системы формулируются по-прежнему в виде оценок переходных процессов (6.5): t_n<t^*_n и σ<σ^*, от которых можно перейти к желаемому распределению корней на комплексной плоскости. На основе выбранных корней формируется желаемое характеристическое уравнение замкнутой системы

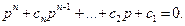(5.42)

Метод синтеза предполагает задание пропорционального состоянию закона управления

(5.43)

где К – матрица неизвестных коэффициентов.

После подстановки алгоритма управления (5.43) в уравнения объекта (5.41) получают уравнения замкнутой системы и записывают ее характеристическое уравнение

Неизвестные коэффициенты матрицы регулятора необходимо определить таким образом, чтобы качество работы замкнутой системы соответствовало заданным оценкам. С этой целью приравнивают характеристическое уравнение замкнутой системы (5.45) желаемому (5.42) и получают соотношения для расчета элементов матрицы К в виде

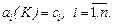(5.46)

Поскольку в общем случае зависимость а_i(К) может быть нелинейной, найти коэффициенты матрицы K по выражению (5.46) не всегда удается даже для одноканального объекта, уравнения которого предварительно записывают в канонической форме.

Часто линейный одноканальный объект удобнее описывать с помощью передаточной функции, поэтому обсудим далее операторную методику модального метода синтеза, предложенную на кафедре автоматики НГТУ.

Постановка задачи синтеза для одноканального объекта. Рассмотрим объект управления, поведение которого описывает передаточная функция

(5.47)

Модальный метод синтеза обеспечивает заданную реакцию системы на начальные условия, которая определяется корнями характеристического уравнения. Корни, в свою очередь, выбираются на основе требований, предъявляемых к динамике в виде условий (5.5). Кроме этого, необходимо, чтобы в статике выполнялось условие (5.4), т. е.

lim y(t) = v

с точностью

.

Таким образом, задача синтеза заключается в обеспечении в замкнутой системе желаемого распределения корней и требуемой статики.

Для ее решения предлагается использовать регулятор, который состоит из двух составляющих: последовательного звена W_s(p) на входе и звена с передаточной функцией W_d(p) в цепи локальной обратной связи. Таким образом, структурная схема замкнутой системы задана и имеет вид, представленный на рис. 5.13.

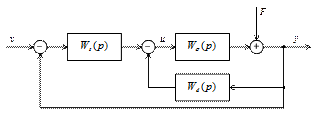
Рис. 5.13. Расчетная структурная схема замкнутой системы

Исходя из их предназначения, звено прямого канала с передаточной функцией W_s(p) будем называть корректором статики, а звено с передаточной функцией W_d(p) - корректором динамики.

Процедура синтеза включает в себя рекомендации по определению параметров этих передаточных функций.

Рассмотрим последовательно этапы модального метода синтеза системы регулирования.

Выбор корректора статики. Для обеспечения условия статики (5.4) при произвольном возмущении M(t), т.е. выполнения свойства lim y(t) = v, предлагается в качестве корректирующего звена W_s(p) использовать интегратор

(5.48)

где k_s – коэффициент усиления регулятора, его численное значение будет определено позже.

Полагая, что объект и корректор динамики не содержат интегрирующих звеньев, покажем выполнение условия (5.4). С этой целью запишем операторное выражение для выходной величины

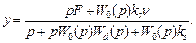(5.49)

Поскольку в статике передаточные функции W₀(p) и W_d(p) «вырождаются» в коэффициенты усиления, получим окончательно y = v.

Таким образом, использование корректора статики W_s(p) вида (5.48) делает систему астатической, и условие (5.4) можно обеспечить с ошибкой А⁰ = 0.

Расчет корректора динамики. В качестве корректора динамики предлагается выбирать звено со следующей передаточной функцией:

, (5.50)

где В(р) - полином числителя передаточной функции объекта W₀ (p), a D(p) - введенный расчетный полином с неизвестными коэффициентами d_i, .

Суть модального метода синтеза заключается в приравнивании действительного и желаемого характеристических уравнений замкнутой системы и вычислении из полученных соотношений параметров регулятора.

Первоначально определим характеристическое уравнение системы, структурная схема которой приведена на рис. 5.18:

. (5.51)

С учетом (5.47), (5.48) и (5.50) уравнение (5.51) принимает вид

причем его порядок равен (n +1).

Подставляя вместо А(р), D(р) и В(р) их выражения, получим действительное характеристическое уравнение замкнутой системы в следующей форме:

(5.52)

Теперь на основе требований к качеству переходных процессов (заданного перерегулирования σ^* и быстродействия t^*_n сформируем желаемое характеристическое уравнение того же порядка, что и (5.52). Для его конструирования используем корневые оценки переходных процессов, с помощью которых получим эталонное распределение корней на комплексной плоскости.

Предварительно определим границу расположения желаемых корней системы. Она зависит от заданного времени переходного процесса t^*_n (оценка (5.36)) и приближенно может быть найдена по соотношению

. (5.53)

Заданное перерегулирование σ* ограничивает сектор на комплексной плоскости, внутри которого должны располагаться желаемые корни (рис. 5.14).

Рис.5.14. К определению области расположения корней

С этой целью по соотношению

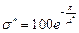
определяется требуемое значение колебательности процессов в системе μ^*, а затем вычисляется значение мнимой части корней с «максимальным» размахом:

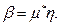(5.54)

Эталонные корни λ₁*,..., λ* _{n +1} могут выбираться внутри ограниченной области комплексной плоскости (рис. 5.19) произвольным образом. Однако чем дальше они удалены от границы η, тем меньше длительность переходного процесса и больше потребуется ресурс управления объекта. Поэтому рекомендуется выбирать корни λ₁*,..., λ* _{n +1} достаточно близко друг к другу и правой границе области расположения корней, а затем сформировать желаемое характеристическое уравнение следующим образом:

(5.55)

Характеристическое уравнение (5.55) запишем в стандартном виде

. (5.56)

Приравнивая коэффициенты при соответствующих степенях оператора р желаемого (5.56) и действительного (5.52) характеристических уравнений системы, запишем выражения для определения неизвестных параметров регулятора:

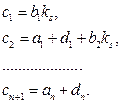(5.57)

Полученные из (5.57) расчетные соотношения имеют вид

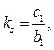
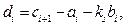
Таким образом, мы определили параметры передаточных функций W_s(p) и W_d(p) регулятора, обеспечивающего в системе требуемые свойства в статике и динамике.

Пример 5.8. Поведение одноканального объекта описывает передаточная функция

Требуется синтезировать систему, в которой качество процессов будет отвечать следующим требованиям: t_n < 3 с; σ = 0, Δ° =0.

Решение. Для определения параметров регулятора используем операторную процедуру модального метода синтеза, структурная расчетная схема которого приведена на рис. 5.18.

В качестве корректора статики используем интегрирующее звено с передаточной функцией W_s(p) = k/р, что гарантирует нулевую статическую ошибку в системе. С целью обеспечения требуемых динамических свойств формируем корректор динамики в виде

.

Здесь k, d₁, d₀ – неизвестные коэффициенты регулятора, которые требуется определить.

Используя структурные преобразования, запишем характеристическое уравнение замкнутой системы (см. рис. 5.17):

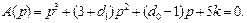
Сформируем теперь желаемое характеристическое уравнение третьего порядка. Предварительно выберем распределение корней, обеспечивающее заданное качество процессов. Поскольку в системе не допускается перерегулирование, корни должны быть вещественными и располагаться на расстоянии не ближе от мнимой оси. В результате выберем следующие корни:

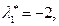
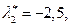
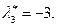
В соответствии с (5.55) получим желаемое характеристическое уравнение

Запишем расчетные соотношения (5.57):

Отсюда находим параметры d₁ = 4,5, d₀ = 19,5, k = 3. Следовательно, пере­даточные функции регулятора имеют вид

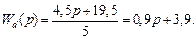
Реализация регулятора. Рассмотрим возможность реализации регулятора, рассчитанного модальным методом. Реализовать корректор статики с передаточной функцией W_s(p), представляющей собой обычный интегратор, не вызывает затруднений. Остановим­ся подробнее на реализации звена обратной связи с передаточной функцией W_d(p).

Поскольку для реальных объектов управления степень полинома числителя передаточной функции W₀(p) обычно меньше степени полинома ее знаменателя (т < n), корректор динамики

как правило, имеет форсирующий характер. Это означает, что необходимо реализовать дифференцирующие звенья, которые усиливают влияние высокочастотной помехи.

С целью уменьшения этого влияния предлагается использовать специальный фильтр, который подключается параллельно объекту и состоит из модели W_m(p) (с выходом 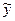) и стабилизирующей добавки L(p) (рис. 5.20). Его называют фильтром Калмана – Бьюсси или параллельным фильтром.

Здесь передаточная функция параллельной модели W_m(p)= W₀(p). Стабилизирующая добавка L (р) «сводит» к нулю разницу между выходом объекта у и выходом модели .

Исследуем свойства фильтра, записав выражение для ошибки

Рис. 5.20. Схема подключения фильтра

которое после преобразований имеет вид

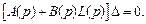
Характеристическое уравнение фильтра следующее

В случае, когда его корни имеют отрицательную вещественную часть, имеет место Δ→0 при t→∞. Таким образом, начиная с некоторого момента времени выход модели у будет повторять выход объекта 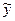как угодно точно. С помощью стабилизирующей добавки L (р) можно получить устойчивые процессы в фильтре и для неустойчивого объекта.

Выбирая соответствующим образом L (р), можно ускорить процесс оценки переменной объекта.

Использование параллельного фильтра позволяет получить схему реализации корректора динамики, изображенную на рис. 5.16. Эту схему можно упростить, если представить передаточную функцию модели в виде произведения

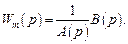(5.60)

После несложных структурных преобразований получим окон-

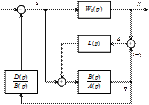
Рис. 5.16. Схемная реализация корректора динамики

чательно структурную схему реализации замкнутой системы (рис. 5.17).

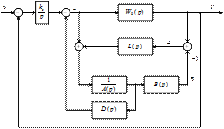
Рис. 5.17. Структурная схема системы с регулятором

Передаточные функции фильтра и регулятора могут быть реализованы на активных элементах после их представления в виде цепочки интеграторов с прямыми и обратными связями согласно первой канонической форме (сигнальный граф в форме с фазовой переменной).

Процедура синтеза регулятора модальным методом. На основе рассмотренной операторной методики модального метода синтеза можно предложить следующую процедуру расчета регулятора.

1. Проверяются условия разрешимости задачи синтеза для исходного объекта управления.

2. Записывается передаточная функция корректора статики W_s(p)=k/p.

3. Выбирается передаточная функция корректора динамики

,

где В(р) - полином числителя передаточной функции объекта; п – порядок объекта; k_s, d_i - коэффициенты регулятора, численные значения которых должны быть определены в процессе синтеза .

4. В соответствии со структурной расчетной схемой (см. рис. 5.13) находится действительное характеристическое уравнение системы, содержащее неизвестные параметры регулятора (5.52).

5. С учетом требований к качеству переходных процессов (σ* иt_n*) формируется желаемое характеристическое уравнение системы (n +1)-го порядка в виде (5.56).

6. Приравниваются коэффициенты при соответствующих степенях оператора р желаемого (5.56) и действительного (5.52) характеристических уравнений системы, записываются расчетные соотношения для параметров регулятора (5.57).

7. В случае, когда степени полиномов числителя и знаменателя передаточной функции объекта связаны соотношением т = (n -1), передаточная функция корректора динамики содержит в числителе и знаменателе полиномы одного порядка. Такой регулятор может быть непосредственно реализован в виде цепочки интеграторов с прямыми обратными связями.

8. В ситуации, когда т < (п –1), корректор динамики представляет собой форсирующее звено, для его реализации в систему следует вводить специальный фильтр (см. рис. 5.16).

9. При расчете стабилизирующей добавки L(p) используется методика модального метода синтеза. Сначала формируется желаемое характеристическое уравнение фильтра так, чтобы процессы в нем заканчивались на порядок быстрее, чем в системе (т. е. t_ф^* ≈ 0,1 t _п*). Приравниваются коэффициенты при coответствующих степенях оператора р полученного желаемого и дейст­вительного (6.59) характеристических уравнений фильтра, записываются соот­ношения для расчета параметров стабилизирующей добавки.

10. Параллельная модель W_m(p) и стабилизирующая добавка L(p) реализуются в виде цепочки интеграторов, из внутренних переменных модели формируется форсирующий регулятор.

Пример 5.9. Предложить схемную реализацию регулятора, рассчитанного для объекта с передаточной функцией

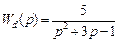
из примера 5.8.

Найденные из условия требуемого качества процессов в замкнутой системе передаточные функции регулятора имеют вид:

где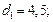

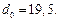
Как видим, корректор динамики представляет собой форсирующее звено первого порядка, поэтому для его реализации введем в систему стабилизирующую добавку с передаточной функцией

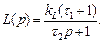
С учетом передаточной функции модели объекта

запишем действительное характеристическое уравнение фильтра (5.59) в виде

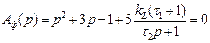
или

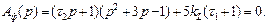
Представим это уравнение в стандартной форме

.

Сформируем желаемое характеристическое уравнение фильтра так, чтобы процессы в нем заканчивались на порядок быстрее, чем в системе. При этом выберем t_ф^* = 0.1, t _п* = 0,3 с.

Поскольку в системе не допускается перерегулирование, сохраним это условие и для фильтра. Таким образом, корни должны быть вещественным и располагаться на расстоянии не ближе от мнимой оси. В результате выберем следующие корни: 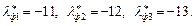Запишем желаемое характеристическое уравнение фильтра

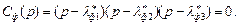
В результате подстановки численных значений корней получим

Определим расчетные соотношения для параметров стабилизирующей добавки, для чего приравняем коэффициенты уравнений

А_ф (р) и С_ф (р):

,

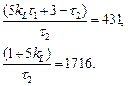
Отсюда найдем k _L =10.2, τ₁=0.2, τ₂=0.03.

Таким образом, передаточная функция стабилизирующей добавки имеет вид

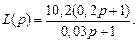
В соответствии с рекомендациями п. 3.6.1 и структурной схемой, представленной на рис. 5.21, приведем на рис. 5.22 полную структурную схему системы с учетом реализации регулятора. На схеме пунктиром выделены: W_m (p) - параллельная модель; L(p) - стабилизирующая добавка; D(p) - полином числителя корректора динамики.

Рис. 5.22. Структурная схема системы для примера 5.9

ЗАКЛЮЧЕНИЕ

На этом заканчивается изложение основных положений линейной теории управления. Возвратимся теперь к вопросу, поставленному во введении: зачем эта дисциплина студентам смежных специальностей? Если к концу чтения настоящего пособия у студентов не возникло понимания необходимости изучения этой дисциплины, автор полагает, что время, потраченное на ее изучение, израсходовано впустую. В качестве оправдания такого состояния можно лишь привести древнюю мудрость: всякое знание должно упасть в подготовленную почву, только тогда оно даст всходы. Вряд ли положение о том, что почву нам еще готовить и готовить, вызовет у кого-нибудь серьезные возражения.

Ну, а те, кто осознал – наверняка смогут объяснить любому, желающему услышать, что в междисциплинарном предмете «Основы теории управления» мы рассмотрели некоторые системные вопросы, пригодные для применения в любой предметной области. И теперь будущие специалисты, как в области вычислительной техники, так и программирования и системного анализа могут взглянуть на свои предметные области с системных позиций. И было бы здорово, наверное, понять, что такое передаточная функция программной системы или переходная функция вычислительной системы. И как переложить предлагаемые теорией управления методы синтеза систем на язык любой из предметных областей. И что такое частотная характеристика разработанной программы. Да мало ли какие проблемы предметных областей можно было бы рассмотреть с общесистемных позиций!

Но даже если указанные вопросы и не будут рассмотрены подобным образом, автор надеется, что изучение основ теории управления внесет свой вклад в развитие кругозора будущего инженера, его интеллекта и миропонимания. И если это случится, то можно считать, что труд, потраченный как на написание этого пособия, так и на его изучение не пропали даром. Да будет так!

Библиографический список

1. Андреев Ю.Н. Управление конечномерными линейными объектами. –M.: Наука, 1978.

2. Бесекерский В.А., Попов Е.П. Теория автоматического регулирования. –М.: Наука, 1974.

3. Ерофеев А. А. Теория автоматического управления. – СПб.: Политехника, 1998.

4. Иващенко Н.Н. Автоматическое регулирование. – М.: Машиностроение, 1978.

5. Коновалов Г.Ф. Радиоавтоматика. – М.: Высш. шк., 1990.

6. Первозванский А.А. Курс теории автоматического управления. –М.: Выс. шк., 1986.

7. Попов Е.П. Теория линейных систем автоматического регулирования и управления. –М.: Высш. шк., 1989.

8. Теория автоматического регулирования. Кн. 1-3 / Под ред. В.В. Солодовникова. – М.: Машиностроение, 1967.

9. Теория автоматического управления. В 2 ч. / Под ред. А.А. Воронова. –М.: Высш. шк., 1986.

10. Топчеев Ю. М. Атлас для проектирования систем автоматического регулирования. –М.: Машиностроение, 1989.

11. Филипс Ч., Харбор Р. Системы управления с обратной связью. –М.: Лаборатория базовых знаний, 2001.

12. Востриков А.С., Французова Г.А. Теория автоматического регулирования. –М.: Высш. шк., 2001.

Дата добавления: 2014-01-15