Лекция 16. Статический анализ скалярных систем

Статический анализ скалярных систем. Пусть имеем систему управления с операторным представлением структурной схемы, приведенным на рис. 4.32.

Рис. 4.32. Операторное представление структурной схемы

системы управления

Ошибка системы имеет две составляющие: по каналу возмущения и по каналу управления

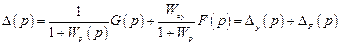, (4.30)

где

(4.30, а)

– передаточная функция разомкнутой системы, – изобра-

жение ошибки от управляющего сигнала, 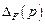– изображение ошибки от возмущающего воздействия.

Рассмотрим условия, при которых эти составляющие минимальны.

1. Ошибка от закона управления. В установившемся режиме

()

,

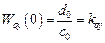
и при единичном ступенчатом входном сигнале (, 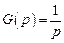) выражение (4.30, а) приобретает вид

.

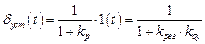Отсюда следует, что

- ошибка принципиально не может быть равной нулю, т.е. система – астатическая;

- с ростом уменьшается, с одной стороны , а с другой - устойчивость: система может оказаться неустойчивой при , где – критический коэффициент усиления разомкнутой системы, при котором замкнутая система находится на границе устойчивости.

Поэтому при проектировании системы задается допустимая величина ошибки, а по ней определяется необходимый статический

коэффициент усиления разомкнутой системы

,

из которого определяется коэффициент регулятора

(изменить 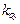нельзя, он принадлежит объекту управления!).

Если передаточная функция разомкнутой системы имеет n-кратный нулевой корень

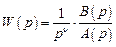
(последовательное соединение регулятора с n интеграторами), то

.

Оценим условия, при которых последнее равенство соблюдается. Пр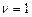и и 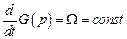получим

,

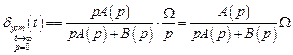т.е. ошибка пропорциональна скорости изменения сигнала управ-

ления (т.е. ошибка – скоростная, а система астатическая с астатизмом первого порядка). В установившемся режиме

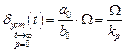. (4.30, б)

Определение этой ошибки производится в режиме изменения входного сигнала с постоянной скоростью (режим постоянной заводки) (рис. 4.33)

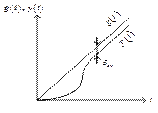
Рис. 4.33. Режим постоянной заводки следящей системы

Точно также при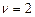

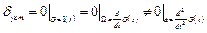
и т.д. Однако с увеличением n система становится структурно неустойчивой (), поэтому становится необходимым применение дополнительных корректирующих звеньев (рис. 4.34).

Рис. 4.34. Годографы астатических систем

2. Ошибка по каналу возмущения в общем случае определяется выражением

.

Пр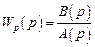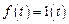и , и 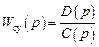(нулевые корни отсутствуют) величина ошибки от возмущения в установившемся режиме равна

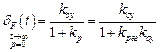
и может быть уменьшена путем увеличения за счет увеличения составляющей 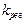(но не !).

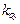Если регулятор и объект – астатические, т.е.

,

,

то

.

При постоянном сигнале возмущения 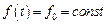в соответствии с теоремами о начальном и конечном значениях:

и

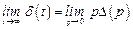
и изображение возмущающего воздействия по Лапласу есть

,

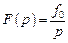а установившаяся ошибка от возмущающего воздействия в установившемся режиме

,

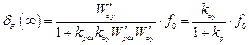т.е. в замкнутой системе ошибка от возмущения в раз меньше, чем в разомкнутой.

Если регулятор статический

,

а объект астатический с астатизмом 1 -го порядка

,

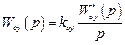то ошибка от возмущающего воздействия

,

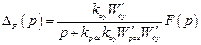а ее установившийся оригинал при :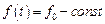

,

т.е. установившаяся ошибка от возмущающего воздействия обрат-

но пропорциональна коэффициенту передачи регулятора.

Если, наконец, регулятор астатический

,

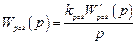а объект также астатический

,

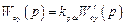то , т.е. статическая ошибка от возмущения отсутствует.

Коэффициенты ошибок. Если изображение внешнего воздействия представлено дробно-рациональной функцией от p, не имеющей кратных корней, то вынужденная составляющая ошибки может быть найдена как степенная функция (2.16΄). Расчет ее может быть значительно упрощен, если внешнее воздействие представлено степенным рядом. Расчет вынужденной составляющей ошибки в этом случае производится методом коэффициентов ошибки. Рассмотрим использование этого метода для случая, когда внешним воздействием является управляющее воздействие .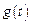

Если входное воздействие 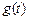имеет произвольную форму, но имеет конечное число 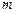производных

,

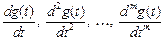то выражение для ошибки управления

можно разложить в ряд Тейлора по степеням комплексной величины :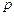

.

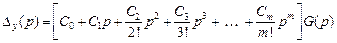Переходя в последнем выражении к оригиналу, получаем формулу для определения установившейся ошибки по управлению

(4.31)

Коэффициенты

, ,

, …,

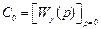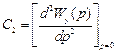называются коэффициентами ошибок и определяются по общему разложению функции в ряд Тейлора по степеням :

– в статических системах коэффициент

– в астатических системах с астатизмом 1-го порядка , ;

– в астатических системах с астатизмом 2-го порядка 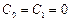, и т.д.

Пример 4.6. Определить коэффициенты ошибок по управляющему воздействию, если передаточная функция разомкнутой системы имеет вид

.

Решение. Передаточная функция по ошибке

.

Определим коэффициенты ряда Тейлора:

,

,

.

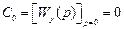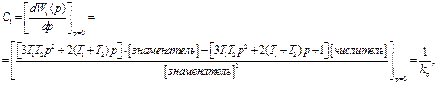
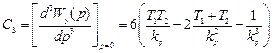Если управляющее воздействие меняется по закону

,

то установившаяся ошибка из выражения (4.31) будет иметь вид

.

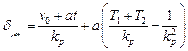При 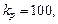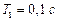, величина установившейся ошибки определяется выражением

,

из которого можно определить величину параметра a, обеспечивающую заданное минимальное значение установившейся ошибки:

.

■

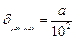Интегральные показатели качества не оценивают устойчивость, а лишь дают возможность сравнительной оценки качества двух процессов управления, т.е. их применяют для заведомо устойчивых процессов. При этом функции времени 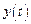абсолютно интегрируемы, т.е. стремятся к нулю. Интегральные показатели качества – это функционалы, в которых роль независимой переменной играют функции времени 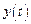, t ³ 0:

.

Функция F подбирается так, чтобы несобственный интеграл сходился, а значения J количественно характеризовали качество процессов 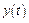. Интегральные показатели качества оценивают процессы в наиболее сжатом виде – кривой 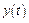ставится в соответствие число, при этом большей сходимости процесса соответствует меньшее значение J для определенного t. В качестве интегральных показателей наиболее часто используются:

– линейный интегральный показатель;

– квадратичные интегральные показатели.

Линейный интегральный показатель качества определяется как площадь, ограниченная кривой процесса, определяемая интегралом

и показанная на рис. 4.35. Если процесс не меняет знака, то площадь под кривой тем меньше, чем быстрее затухает процесс.

Рис. 4.35. Линейный интегральный показатель качества

Обобщениями линейного интегрального показателя являются моменты

, i = 0, 1, 2…,

для вычисления которых производится интегрирование «с весом»: ординаты при бóльших значениях t «стóят» больше. Моменты легко вычисляются по изображению переменной 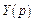, если воспользоваться теоремой о дифференцировании изображения

.

В частности, при p = 0 получаем

.

Очевидно также, что

.

Недостатком линейного интегрального показателя и моментов

является то, что они характеризуют только процессы, не меняющие знак.

Интегральный квадратичный показатель описывается выражением

и имеет тем меньшее значение, чем быстрее процесс приближается к идеальному, для которого I ₀ = 0.

Использованием формулы обращения по Лапласу интегральный квадратичный показатель может быть представлен в виде

(в устойчивых системах абсцисса сходимости равна нулю). Поменяем порядок интегрирования

.

Под интегралом имеем произведение рациональных функций, для вычисления которого можно использовать известные формулы для конкретных степеней n полиномов знаменателей:

– n = 1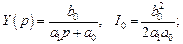

– n = 2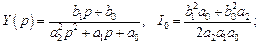

– n = 3

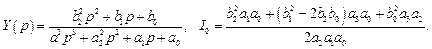
В общем случае для вычисления интегральных квадратичных

показателей можно использовать алгоритм Некольны–Острема (Острем К. Введение в стохастическую теорию управления. – М.: Мир, 1973).

Если положить p = jω, то получим

.

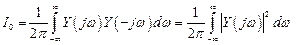Это соотношение называется формулой Парсеваля. Она означает, что энергия движения процесса пропорциональна интегралу от квадрата модуля спектральной функции этого процесса.

Недостатком квадратичного показателя качества является игнорирование им колебательности процесса. Между тем системы с меньшим значением интегрального квадратичного показателя оказываются колебательными в большей степени.

Пример 4.7. Рассмотрим систему с отрицательной единичной обратной связью, передаточная функция разомкнутого контура которой есть

.

Передаточная функция замкнутой системы от задающего воздействия до переменной ошибки 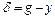выглядит как

.

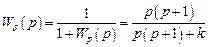Изображение переменной ошибки Δ(p) при задании ступенчато-

го единичного воздействия есть

.

Выражение интегрального квадратичного показателя качества переходного процесса для n = 2 по приведенной выше формуле есть

.

Из полученной зависимости следует, что значение показателя качества уменьшается с увеличением коэффициента усиления контура; при k → ∞ .

Рассматриваемая система устойчива при любом k, т.к. коэффициенты характеристического полинома 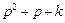положительны (для n = 2 это является необходимым и достаточным условием). Однако стремление к уменьшению интегрального квадратичного показателя качества путем увеличения коэффициента усиления контура ведет к росту колебательности процесса.

В самом деле, выражение для колебательности корней μ (отношение абсолютных значений их мнимой и действительной частей), получаемое на основе выражения для вычисления корней характеристического полинома

есть

,

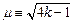откуда следует, что с ростом k колебательность корней растет, а относительное затухание процессов уменьшается. При этом абсолютное затухание остается неизменным.

Такой результат имеет место потому, что экстремалью функционала является идеальный процесс, затухающий мгновенно. Стремление к такому процессу в реальной динамической системе и дает такой результат.

■

Для учета колебательности процесса интегральный квадратич-

ный показатель дополняют взвешенным интегралом от квадрата производной функции времени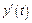

.

В результате получаем улучшенный интегральный квадратичный показатель. При колебательном процессе ординаты переменной становятся значительными и оказывают свое влияние на значение функционала I ₁.

Улучшенная интегральная квадратичная оценка тем меньше, чем ближе процесс 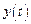к некоторой экстремали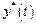, определяемой на основе следующих рассуждений. Преобразуем I ₁ к виду

,

в котором второе слагаемое представим так

.

Здесь учтено, что , а .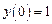

Функционал I ₁ достигает минимума, если первая составляющая равна нулю

,

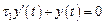т.е. если 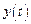является решением дифференциального уравнения первого порядка при начальном условии , когда

.

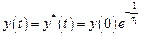Эта кривая – экстремаль функционала I ₁ – приведена на рис. 4.36.

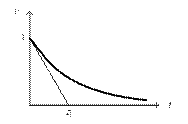
Рис. 4.36. Безусловная экстремаль улучшенного интегрального показателя

Максимальное значение функционала при типовом начальном условии 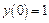равно

.

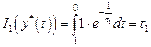Чем лучше система управления в смысле показателя I ₁, тем ближе к экспоненте с постоянной времени τ ₁ процесс 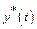. Увеличение τ ₁ при формировании показателя эквивалентно выбору системы с медленнее затухающими процессами, т.е. показатель I ₁ пропагандирует в качестве эталонной систему управления первого порядка.

В системах высокого порядка процесс 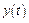отличается от экспоненты 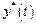на величину разности

,

имеющей смысл расстояния между кривым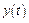и и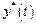. По величине можно судить о величине расхождений между реальным процессом 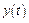и экспонентой 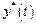. Для этого определяются верхнее (мажоранта) и нижнее 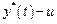(миноранта) допустимые отклонения, в которые укладывается процесс, как показано на рис.4.37.

Рис. 4.37. Мажоранта и миноранта процессов

Оказывается, что для улучшенной интегральной квадратичной оценки величина u определяется из соотношения

,

.

Чем больше τ ₁, тем уже полоса, в которую заключена оцениваемая кривая 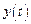, однако тем больше и величина I ₁. Поскольку , то задавая различные значения τ ₁, можно добиться наилучшей оценки прямых показателей качества процесса 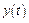через интегральный показатель качества .

Дата добавления: 2014-01-15