Определение реакций в однопролетных статически неопределимых стержневых элементах

Канонические уравнения метода перемещений

Основная система метода перемещений

Степень кинематической неопределимости системы

Метод перемещений.

Для раскрытия сути метода перемещений дадим определение понятия степени кинематической неопределимости. Степенью кинематической неопределимости называется число возможных перемещений узлов заданной системы.

Как это было показано выше, при расчете статически неопре­делимых систем по методу сил искомыми величинами принима­лись усилия в лишних связях (силы и моменты). После определе­ния неизвестных усилий в лишних связях далее по методу сечений определяются внутренние усилия в произвольном сечении и через них устанавливаются величины перемещений в любой точке конст­рукции. При расчете статически неопределимых систем по методу перемещений за искомые величины принимаются те перемещения, через которые можно будет определить величины внутренних уси­лий в любом произвольном сечении. При расчете стержневых сис­тем по классическому методу перемещений, принимая за искомые величины пере­мещения узлов заданной системы, при их определении пренебрегаются деформации от попе­речных и продольных сил ввиду их малости и учитываются лишь деформации от изгиба в элементах заданной системы. Кроме того, пренебрегаются различием длин элементов заданной системы до и после нагружения системы.

Известно, что для определения изгибающего момента в произ­вольном сечении заданного стержня необходимо знать величины поворотов в концевых сечениях и относительные линейные смеще­ния концов стержня друг относительно друга.

При расчете статически неопределимой системы методом пере­мещений первоначально необходимо установить общее число неиз­вестных перемещений, подлежащих определению для адекватного вычисления величин внутренних усилий.

Следовательно, при расчете рам за неизвестные следует прини­мать углы поворотов и линейные смещения узлов заданной систе­мы. Общее число неизвестных n будет равно сумме числа неизвест­ных углов поворота узлов n_у и их возможных линейных переме­щений n_л , т.е.

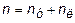. (2.15)

Число неизвестных углов поворота n_у равно числу жестких узлов заданной системы. Жестким считается узел, в котором кон­цы, по крайней мере, двух из сходящихся в нем стержней жестко связаны между собой (например, узлы 1, 2, 3, на рис. 1, а; узлы 1, 2 на рис. 2., a).

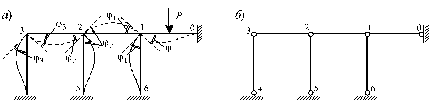
Рис.1.

Для определения числа линейных неизвестных перемещений заданную систему следует заменить ее шарнирной схемой пу­тем введения полных шарниров во все узлы и опорные закрепле­ния (рис 1, б и рис. 2., б). Число неизвестных линейных сме­щений узлов системы равно числу стержней, которые необходимо ввести в шарнирную схему, чтобы превратить ее в геометрически неизменяемую систему. Следовательно, число независимых линей­ных смещений узлов равно степени геометрической изменяемости шарнирной системы, полученной из заданной, путем введения во все жесткие узлы, включая и опорные, полных шарниров.

На основании о пренебрежении продольными деформациями элементов, для плоской рамы (рис. 1, а), линейные смещения узлов отсутствуют. При этом, шарнирная схема (рис. 1, б) является геометрически неизменяемой.

Рис.2.

Рамы, шарнир­ные схемы которых являются геометри­чески неизменяемы­ми, относятся к ка­тегории, так называ­емых, закрепленных или несвободных. Для таких рам число неизвестных перемещений легко определяется и оно всегда равно числу жестких узлов: n = n_y. В нашем примере n = 3.

В качестве другого примера, рассмотрим раму, изображенную на рис. 2., a, число жестких узлов которого равно 2. Следова­тельно, n_у = 2.

Шарнирная схема рамы один раз геометрически изменяемая, так как для превращения ее в геометрически неизменяемую необ­ходимо ввести 1 стержень, например, так, как это показано на рис. 2., б. Итак, число линейных неизвестных перемещений n_л = 1. Общее число неизвестных перемещений в рассматриваемой системе, изображенной на рис. 2., a, равно n = 2 + 1 = 3.

Дата добавления: 2014-01-15