Канонические уравнения метода перемещений

С учетом принятых обозначений, суммарную реакцию в i-ой дополнительно введенной связи, можно записать в следующем ви­де:

R_i = r_i1 Z₁ + r_i2 Z₂ +... + r_in Z_n + R_iPq (i = 1, 2,..., n). (2.17)

Для того, чтобы основная система стала эквивалентна задан­ной, полную реакцию R_i (i = 1, 2,..., n) во всех введенных связях основной системы, согласно (2.16), необходимо приравнять нулю:

, (i = 1,2,3,...,n),

или в развернутой форме:

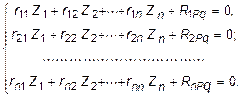(2.18)

Здесь неизвестными являются перемещения Z_i (i = 1, 2,..., n), т.е. возможные перемещения узлов заданной системы по направле­нию введенных связей в основной системе.

Уравнения (2.18) называются каноническими уравнения­ми метода перемещений. Коэффициенты этих уравнений обладают свойством симметрии r_ik = r_ki , что следует из теоремы о взаимности реакций, примененной к основной системе ме­тода перемещений.

Проверкой правильности расчета рамы методом перемещений служат равенство нулю суммы моментов, передающихся на каждый узел с примыкающих к нему стержней, а также иные условия равновесия рамы.

Заметим, что в методе сил эти условия выполняются в каждой единичной эпюре и поэтому не обеспечивают проверку решения канонических уравнений.

Для определения коэффициентов r_ik и свободных членов R_iPq системы канонических уравнений метода перемещений (2.18) необ­ходимо предварительно построить эпюры моментов в основной системе от заданной системы внешних сил и от единичных переме­щений Z_i = 1. Все коэффициенты, а также свободные члены урав­нений разделяются на две группы: коэффициенты и свободные члены, представляющие реактивные моменты во введенных допол­нительных элементах; коэффициенты и свободные члены, пред­ставляющие реактивные усилия во введенных дополнительных эле­ментах основной системы.

Коэффициенты и свободные члены, представляющие реактив­ные моменты во введенных элементах, определяются вырезанием узлов и составлением уравнений равновесия моментов SМ = 0, со­гласно методу сечений.

Коэффициенты и свободные члены, представляющие реактив­ные усилия во введенных связях основной системы определяются разрезанием элементов рамы и составлением уравнения равновесия сил на отсеченной части Sy = 0. При этом направление оси y вы­бирается так, чтобы уравнение получилось наиболее простым по форме.

Следовательно, для того, чтобы построить эпюру моментов в основной системе от действия системы внешних сил и от Z_i = 1 (i = 1, 2,..., n), необходимо предварительно определить эпюру мо­ментов в однопролетных статически неопределенных стержнях (входящих в состав основной системы, за исключением дополни­тельных элементов). Откуда следует, что в общем случае для реали­зации метода перемещений необходимо предварительно рассмот­реть решение задачи об определении эпюр внутренних усилий в однопролетных статически неопределимых стержнях при кинема­тическом (линейном и угловом перемещении концевых сечений) и внешнем силовом и температурном нагружении.

Дата добавления: 2014-01-15