
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение реакций в однопролетных статически неопределимых стержневых элементах
|
|
|
|
Сначала определим выражения изгибающих моментов и поперечных сил в однопролетных балках при единичных угловых перемещениях или при единичных относительных линейных смещениях концевых сечений (рис. 4, а).
Дифференциальное уравнение изгиба балок с постоянным поперечным сечением при отсутствии внешних нагрузок, действующих в пролете, записывается в виде:
 Рис.4
Рис.4
|
 . (2.19)
. (2.19)
Общее решение однородного дифференциального уравнения (2.16) запишем в следующем виде:

 , (2.20)
, (2.20)
откуда
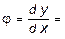
 . (2.21)
. (2.21)
Вводим следующие граничные условия:
при х = 0, у = у0 ; j = j0 ;
при х = l, y = yl ;
j = jl . (2.22)
C учетом граничных условий задачи (2.22) из (2.20) и (2.21), получим:
c4 = у0; c3 = j0; c1 l3 + c2 l2 + j0 l + у0 = yl;
3 c1 l2 + 2 c2 l + j0 = jl . (2.23)
В результате совместного рассмотрения уравнений (2.23) получим выражения произвольных постоянных сi (i = 1,2,3,4), представленное в следующем виде:


Далее определим выражения M и Q:

 (2.24)
(2.24)
Для примера вычислим значения M и Q в концевых сечениях для балки с двумя защемленными концами при j0 = 1. В данном случае имеем: jl = yl = у0 = 0.
Подставляя эти значения в (2.24) получим:
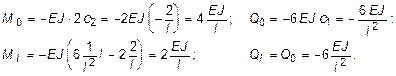
Результаты расчетов эпюры моментов и поперечных сил для однопролетных статически неопределимых балок с различными граничными условиями их закрепления и при различном характере кинематического нагружения обобщены в таблице1.Ординаты эпюры моментов отложены со стороны растянутого волокна.
Для определения эпюры моментов в однопролетных статически неопределимых балочных элементах основной системы от действия внешних сил, удобно применить метод сил.
Так например, однопролетная балка, изображенная на рис. 4, б, трижды статически неопределима. А балка, изображенная на рис. 4, в, один раз статически неопределима. Для удобства, результаты расчетов эпюры моментов однопролетных статически неопределимых элементах, с различными граничными условиями их закрепления, от действия наиболее часто встречающихся силовых и температурных нагружений, обобщены в таблице 1.
При неравномерном нагреве по высоте поперечного сечения балки и при равномерном нагреве по ее длине, изгибающие моменты и поперечные силы определяются согласно общеизвестных выражений:
 ,
,
где - температурный коэффициент линейного расширения; h -высота поперечного сечения; х - независимая переменная 0 £ x £ l; l - длина элемента.
В заключении заметим, что применяя метод перемещений, следует твердо придерживается какого-либо определенного правила знаков. Принять, что углы поворота опорного сечения, а также реактивный момент, действующий на балку со стороны заделки, положительны, если в результате оси поворачиваются по часовой стрелке. Линейное смещение узла принято положительным, если оно совпадает по направлению с положительной реакцией, вызывающей растяжение опорного сечения стержня.
Таблица 1
| № n/n | Схема балки и воздействия на нее | Эпюры изгибающих моментов1) и реакции | Формулы |
| 1. | 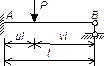
| 
|    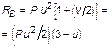
|
| 2. | 
| 
|   
|
| 3. | 
| 
|  
|
| 4. | 
| 
|  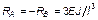
|
| 5. | 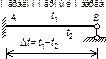
| 
|  2) 2) 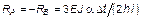
|
| 6. | 
| 
|     
|
| 7. | 
| 
|  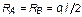
|
| 8. | 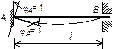
| 
|  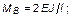 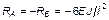
|
| 9. | 
| 
|  
|
| 10. | 
| 
|  2) 2) 
|
Примечание. 1) ординаты отложены со стороны растянутого волокна.;
2) h - высота поперечного сечения; a - температурный коэффициент линейного расширения.
|
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 690; Нарушение авторских прав?; Мы поможем в написании вашей работы!