Пример 2.10.3

Найти наибольшее и наименьшее значения функции
при условии, что x₁, x₂, x₃ удовлетворяют уравнению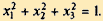

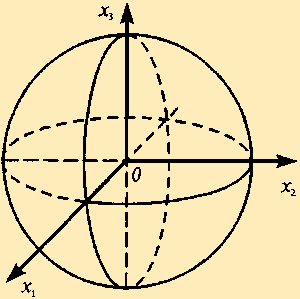
Решение. Уравнение связи определяет в пространстве сферу единичного радиуса с центром в начале координат (2.7). Так как сфера — замкнутое

рис. 2.9

ограниченное множество, то согласно теореме Вейерштрасса функция достигает на ней своего наибольшего и наименьшего значений.
Необходимо найти условный глобальный экстремум. Запишем уравнение связи в виде:

Составим функцию Лагранжа: Найдем частные производные этой функции по x₁, x₂, λ.

Приравняв частные производные нулю, получим систему:

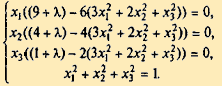
Решая систему, получим стационарные точки, в которых найдем значения функции Z.

Выберем из всех значений z наибольшее и наименьшее: z_наиб. = 1, а z_наим. = 0. Легко видеть, в каких точках сферы достигаются эти значения.

Если число переменных n = 2, нелинейные задачи можно решать геометрически. Ограничения должны быть записаны в виде неравенств

φi (x1, x2) ≤ bi, i = 1, 2,..., m,

(2.41)

а целевая функция иметь вид

z = f(x1, x2)

(2.42)

Как и в случае геометрического решения задач линейного программирования, сначала необходимо построить область допустимых решений (ОДР) — множество точек плоскости, удовлетворяющих неравенствам (2.41). Но в отличие от задач линейного программирования здесь ОДР не обязательно будет выпуклой и может быть даже разрывной. Экстремум функции может достигаться и внутри области, и на границе. После построения ОДР следует записать уравнения линий уровня целевой функции — множество точек плоскости, в которых целевая функция (2.42) постоянна: f(x₁, x₂) = C, и определить направление возрастания (убывания) целевой функции, построив, например, линии уровня для разных значений С.
Затем, перемещая линию уровня в нужном направлении в ОДР, найти точки области, в которых целевая функция принимает оптимальное значение.

Дата добавления: 2014-01-15