Генеалогическое дерево

Деревья

Связность графа

Граф называется связным, если любая пара его вершин связана.
Связными компонентами графа называются подграфы данного графа, вершины которых связаны.

Дерево — это связный граф без циклов.
Деревья особенно часто возникают на практике при изображении различных иерархий. Например, популярны генеалогические деревья.

На рисунке 2.17 показано библейское генеалогическое дерево.

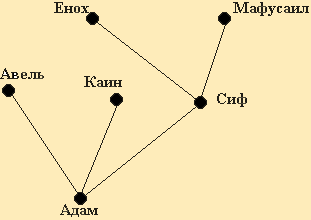
Рис. 2.17

Граф без цикла называется лесом. Вершины степени 1 в дереве называются листьями.
Деревья - очень удобный инструмент представления информации самого разного вида.
Деревья отличаются от простых графов тем, что при обходе дерева невозможны циклы. Это делает графы очень удобной формой организации данных для различных алгоритмов. Таким образом, понятия дерева активно используется в информатике и программировании.

Очевидно, что графический способ представления графов непригоден для ПК. Поэтому существуют другие способы представления графов.

В теории графов применяются

1. Матрица инцинденций. Это матрица А с n строками, соответствующими вершинам, и m столбцами, соответствующнго рёбрам. Для ориентированного графа столбец, соответствующий дуге (х,y) содержит - 1 в строке, соответствующей вершине х и 1, в строке, соответствующей вершине у. Во всех остальных 0. Петлю, т.е. дугу (х,х) можно представлять иным значением в строке х, например, 2. Если граф неориентированный, то столбец, соответствуюший ребру (х,у) содержит 1, соответствующие х и у и нули во всех остальных строках.
2. Матрица смежности. Это матрица n×n где n - число вершин, где b_ij = 1, если существует ребро, идещее из вершины х в вершину у и b_ij = 0 в противном случае.

Составим матрицы инциндентности и смежности для следующего непрерывного графа (рис. 2.18)

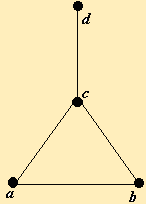Рис. 2.18

Матрица инцидентности

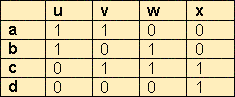
Матрица смежности

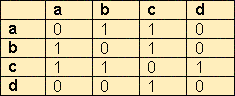
Дата добавления: 2014-01-15