Пример 2.14.1

Алгоритм решения

Нахождение минимального остова в графе

Тема 2.14. Методы решения сетевых задач.

1. Упорядочить ребра графа по возростанию весов;
2. Выбрать ребро с минимальным весом, не образующее цикл с ранее выбранными ребрами. Занести выбранное ребро в список ребер строящегося остова;
3. Проверить, все ли вершины графа вошли в постоенный остов. Если нет, то выполнить пункт 2.

Продемонстрируем приведенный выше алгоритм на примере.

Требуется спроектировать радиотрансляционную сеть, которая должна обслуживать семь населённых пунктов. Расстояния между пунктами приведены в таблице.

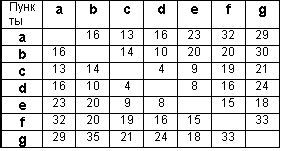
рис. 2.24

Решение
Для решения данной задачи достаточно рассмотреть или только левую или только правую часть от главной диагонали матрицы. Воспользуемся левой частью таблицы.
Из элементов матрицы выбираем минимальный - (D,С) = 4. Обводим выбранный элемент кружком.

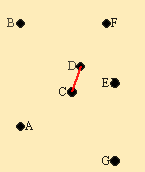рис. 2.25

Из оставшихся элементов выбираем минимальный - (D,E) = 8. Элемент обводим кружком. Чтобы выполнялось условие 2 пункты С и D не должны соединяться, поэтому элемент (Е,С) зачёркивается.

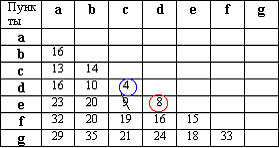
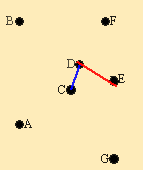рис. 2.26

Из невыделенных и незачеркнутых элементов минимальным является (D,B). Этот элемент обводится кружком. Элементы (С,В) и (Е,В) зачёркиваются.

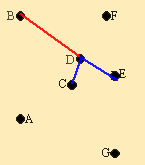рис. 2.27

Минимальным элементом является (С,А) = 13. Элементы (В,А), (D,А) и (Е,А) зачеркиваются.

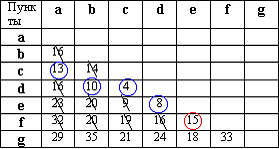
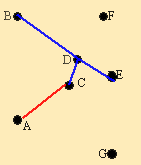рис. 2.28

Из невыделенных и незачеркнутых элементов минимальным является (F,E) = 15. Элементы (F,A), (F,B), (F,C) и (F,D) зачёркиваются.

рис. 2.29

В последней строке минимальным элементом является (G,E) = 18. Обводим этот элемент, и получаем остов, связывающий все семь пунктов. Все остальные элементы вычеркиваются.

рис. 2.30

Длина минимального остова равна (С,А)+(D,B)+(D,С)+(Е,D)+(F,E)+(G,E) = 13+10+4+8+15+18 = 68.

Дата добавления: 2014-01-15