Материал основной части лекции

ПЛАН

проведения занятия

№ п/п	Учебные вопросы занятия	Время, мин.
I. II	Вводная часть: Объявление темы, темы занятия. Постановка учебных целей занятия. Основная часть.	2-3
	1. Предмет и задачи математической статистики. Генеральная и выборочная совокупности. 2. Статистический ряд. Статистический закон распределения случайной величины. 3. Эмпирическая функция распределения. Графическое изображение статистических рядов.
	Заключительная часть	2-3
	Подведение итогов занятия. Выдача задания на самостоятельную работу.

Предмет и задачи математической статистики

Теория вероятностей и математическая статистика занимаются количественным и качественным анализом закономерностей случайных массовых явлений. При изу­чении курса теории вероятностей предполагалось, что ве­роятности наступления отдельных событий известны. Считались известными законы распределения случайных величин или их числовые характеристики. Как правило, на практике вероятности наступления событий, законы распределения случайных величин или параметры этих законов распределения неизвестны.Для их определения (оценивания) необходимо производить эксперимент, спе­циальные испытания.

Математическая статистика разрабатывает методы математической обработки результатов испытания с целью получения сведений о вероятностях наступления отдельных событий, о законах распределения случайных величин или параметрах этих законов.

При обработке результатов экспериментастатистиче­скими методами основные понятия теории вероятно­стей — вероятность наступления случайного события, законы распределения случайных величин, параметры за­конов распределения случайных величин и т. д. высту­пают как некоторые математические модели реальных закономерностей. Таким образом, теориявероятностей разрабатывает математические модели для описанияреальных закономерностей случайных массовых явлений, формирует систему взглядов на статистическую обработ­ку результатов эксперимента.

Основой статистических методов являются экспери­ментальные данные, часто называемые статистическими данными.

Статистическими данными называют сведения о чис­ле объектов, обладающих теми или иными признаками. Например, статистическими данными являются данные отклонений размеров деталей от номинального размера;

данные о прочностных признаках образцов некоторого сорта стали. Перечисленные данные являются числовыми характеристиками массовых случайных явле­ний (сортности деталей, нагрузки АТС, производительно­сти труда), поэтому предметом математической статисти­ки являются случайные явления, а ее основной зада­чей — количественный и качественный· анализы этих явлений.

Основные задачи математической статистики состоят в разработке методов:

1) организации и планирования статистических на­блюдений;

2) сбора статистических данных;

3) «свертки информации», т. е. методов группировки и сокращения статистических данных с целью сведения большого числа таких данных к небольшому числу пара­метров, которые в сжатом виде характеризуют всю иссле­дуемую совокупность;

4) анализа статистических данных;

5) принятия решений, рекомендаций и выводов на основе анализа статистических данных;

6) прогнозирования случайных явлений.

Одним из основных методов статистического наблю­дения является выборочный метод. Рассмотрим основ­ные понятия этого метода.

Генеральная и выборочная совокупности

Пусть для исследования закономерностей случайного явления произведено «n”опытов, в результате которых по-

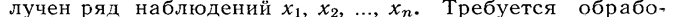
тать этот ряд статистически.

Для любой статистической обработки надо вначале построить математическую модель ряда наблюдений, т. е. указать, какие величины случайны, какие не случайны, какие зависимы, какие не­зависимы и т. д.

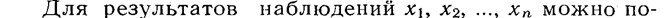
строить различные математические модели. Рассмотрим модель, в которой ряд наблюдений задается формулой

Такую модель можно, например, принять при анали­зе размеров деталей, изготавливаемых на станках-авто­матах. В этом случае смысл параметров модели ряда на­блюдений, задаваемой формулой (1), состоит в следую-

задаваемого формулой (1), можно также делать различ­ные предположения.

Мы будем исходить из наи­более простых предположений относительно функции

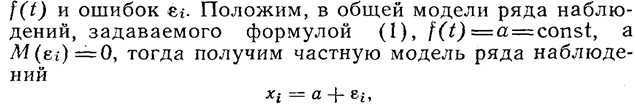
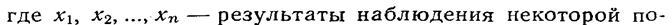
стоянной величины, причем эти результаты организованы таким образом, что систематические ошибки достаточно малы и ими можно пренебречь, а колебания результатов

статистические предположения. Будем считать случаи-

Если эти предположения выполнены, то исследуемое случайное явление, обладающее количественным призна­ком Χ (размер детали, процент бракованных деталей, число отказов элемента некоторого устройства и т. д.), будем рассматривать как одномерную случайную вели­чину X(CB X).

Ставится задача оценить функцию распределения.

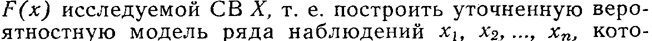
рая бы отражала в себе основные статистические особен­ности этого пяла.

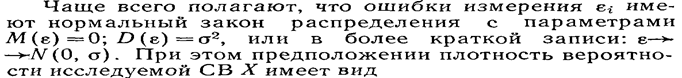
Построив нормальную модель ряда наблюдений, про­изводят оценку параметров α и σ вероятностной модели ряда наблюдений.

Наиболее точные сведения о случайной величине X можно получить, производя максимально возможное ко­личество измерений этой случайной величины.

Дата добавления: 2014-01-15