Свойства делимости целых чисел

Алгоритм Кнута

………………………

;

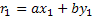
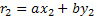
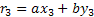
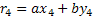
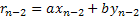
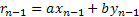
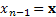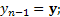
Алгоритм Кнута удобно представлять в виде таблицы

Остаток (r)	q	x	y
A	*	x-1 1	y-1 0
B	*	x0 0	y0 1
r1	q1	x1	y1
r2	q2	x2	y2
…………………..	……………………….	……………………	……………………….
rn-2	qn-2	xn-2	yn-2
rn-1	qn-1	xn-1	yn-1

;

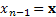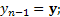
Общий вид:

x_j=x_j-2-q_jx_j-1

y_j=y_j-2-q_jy_j-1

Остаток (r)	q	x	y
a=1234	*
b=54	*
		1-22*0=1
		-1
		1-5*(-1)=6
		-1-1*6= -7

Простые числа

Два числа a и b называются взаимно простыми если их НОД = 1

(a₁,a₂,….,a_n)= НОД

(a₁,a₂) = d₁

(a₃,d₁) = d₂

…………..

(d_n-3,d_n-1) = d_n

a₁*a₂= k*d

Теорема разложения целых чисел (Главная теорема арифметики)

Любое составное число m можно однозначно представить в виде произведения простых сомножителей p, m = p1*p2*…..*p_k

Эта теорема имеет большое прикладное значение в криптографии.

Обозначения:

m – составное число

p - простое

Составное число может раскладываться на простые, при этом могут быть две формы:

1)когда все сомножители разные

2) когда есть кратные сомножители

Пример: m= 720

Применим школьный алгоритм разложения – последовательное деление на возрастающие простые сомножители

Кратность указывается с помощью верхнего индекса 720 = 2⁴*3²*5 - такая форма носит название – каноническое разложение на простые сомножители.

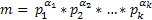Это позволяет при большем числе кратных сомножителей достаточно компактно записать разложение.

С помощью такого «школьного» алгоритма число с большим количеством десятичных знаков можно раскладывать годами.

Это одна из сложных математических задач на которой основаны алгоритмы шифрование/расшифрования с помощью открытого ключа. При секретном ключе данная задача не используется. Вообще шифрование с открытым ключом основано на ряде математически сложных задач. Задач, для которых быстродействующие алгоритмы пока не придуманы. На этом и основана криптостойкость. Эта криптостойкость носит название практической криптостойкости, т.к. как только будут найдены другие быстродействующие алгоритмы разложение, эти алгоритмы потеряют свою актуальность. В перспективе таким возможным алгоритмом может стать алгоритм на основе квантовой физики. Там все процессы идут параллельно и независимо от тако насколько большое число все делается достаточно быстро.

Одним из алгоритмов основанных на решение сложных математических задач, является алгоритм RSA. Этот алгоритм мы рассмотрим в одной из следующих лекций и немножко под другим углом.

Применение этой теоремы это – например для нахождение НОД. Т.е зная разложение, два числа, допустим a и b такие что:

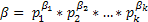
Примечание: При получение разного числа сомножителей можно дописать так называемые «фиктивные» сомножители. н-р: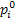

мы можем найти НОД по формуле: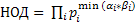

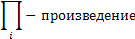
От каждого разложение берется пара сомножителей, выбирается по показателям.

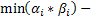из каждой пары сомножителей выбирается сомножитель с минимальным показателем.

Еще один простейший способ нахождения это- решето Эратосфена. Тоже «школьный» алгоритм.

Принцип такой:

имеем ось. начиная от 1 (работаем с натуральными числами) и до некоторого N (в нашем случае допустим 132). И путем просеивания всех составных чисел на этой оси. Сначала берется наименьшее простое число с оси (p= 2) и все числа кратные этому числу (в нашем случае 2) вычеркиваются. Далее берется следующее наименьшее простое число (p=3) и вычеркиваются все числа кратные данному. и.т.д.

1 2 3 4 …………. N=132

Возникает вопрос: Будем мы брать здесь например 17 или 19?

Выбираем числа p по формуле . Т.е. p не должно быть больше чем корень из N.

В конце концов, на оси все составные числа будут вычеркнуты и останутся только простые числа.

Пример

Т.е. 720= 2⁴*3²*5,

а 90= 2*3²*5

Берем минимальные показатели:

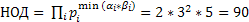- т.е. число 90 является НОД(d) чисел 90 и 720.

Аналогично НОК:

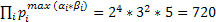- т.е. число 720 является НОК(k) чисел 90 и 720.

Другая сфера приложения это н-р: Имеем некоторое большое число и имеем его разложение и на основе этого надо найти все его делители.

Если кратность в разложение есть то удобно использовать определенный способ нахождения всех делителей.

В общем случае когда составное число раскладывается по канонической формуле все делители можно найти по такой формуле (эта формула тоже обосновывается теоремой)

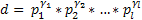- мы имеем разложение

…………….

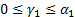
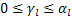
В нашем случае (про 720)

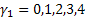
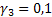
и подставляя всевозможные вариации этих значений мы и получим все делители.

т.е. d = 1,2,4,8,16…………

в нашем случае будет 30 делителей

Еще один вариант приложения разложения. По разложения можно найти сумму всех делителей ()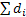

Принято обозначать сумму всех делителей нашего числа а как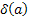

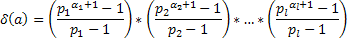
Для нашего примера это будет выглядеть как:

Дата добавления: 2014-01-15