Функция Эйлера

Числовые функции

В теории чисел есть ряд числовых функций зависящих от натуральных чисел. Мы рассмотрим часть этих функций, которые находят широкое применение как в криптоалгоритмах так и в криптоанализе.

Имеется целое, положительное число m. Оно может быть как составным, так и простым.

Функцию Эйлера принято обозначать, практически во всех учебниках как:

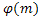
Назначение функции:

Допустим, мы имеем число m – натуральное. Рассмотрим на оси все числа.

1,2,3,4…. m-1 m

Вопрос:

Сколько чисел в диапазоне от 1 до m-1 (m), являются взаимно простыми? (имеют с m НОД=1)

(a,m)=1 – должны быть взаимно простыми. (должны быть взаимно простыми с m)

Если m=p, то взаимно простых будет p-1. Т.к. если число m-простое, то все числа являются для него взаимно простыми, исключая само число m.

Ну а если число m составное?

Эйлер установил такую закономерность, что существует определенная формула, по которой можно вычислить число взаимно простых. (самый простой способ это перебор).

Эта формула определяется на основе разложения числа m.

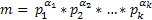- раскладываем на простые сомножители.

Теперь надо использовать только различающиеся сомножители. Пример:

m= 60 = 2*2*3*5; в каноническом виде - 2²*3*5: p₁=2; p₂=3; p₃=5;

Справка: Любое составное число раскладывается однозначно.

Содержательно, Функция Эйлера устанавливает число взаимно простых чисел с заданным числом m.

Есть формула которая учитывает кратность сомножителей, а некоторые не учитывают.

Если все сомножители разные, то это одна формула, а если каноническая, то можно выразить ее через показатели.

Эти две формулы мы и рассмотрим.

Пусть разложение такого, что все сомножители разные.

I) Участвует само число m, затем следует рекуррентное выражение:

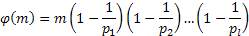
В нашем случае:

;

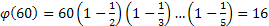Значит, от 1 до 60 находятся 16 взаимно простых чисел с 60.

II)

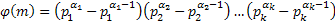
В нашем случае:

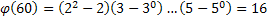
Отметим приложение в криптографии.

В криптографии часто надо вычислять, шифровать по некоторому модулю. Модуль может быть как составным так и простым. Когда модуль составное число, тогда и используется функция Эйлера для однозначного шифрования. Там осуществляется работа с множеством чисел, которые являются взаимно простыми в заданном модулем диапазоне.

Классическое (наиважнейшее) приложение этой функции такое:

Заданно некоторое натуральное число a и заданно некоторое число m, пусть m-составное, натуральное, положительное. Если эти два числа взаимно просты, тогда для этой пары чисел справедлива следующая теорема (теорема Эйлера):

Берем число a, возводим в ,,берем модуль от

т.е. остаток будет равен всегда единице.

Это мы рассматривали нахождением обратных элементов. К этой теореме мы вернемся позже.

Частный случай: m- простое(p), то:

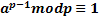
Это теорема малая Ферма, а Эйлер усилил, распространил на все функции Эйлера.

Ограничений у этого частного случая меньше, чем у теореме Эйлера. т.к. тут автоматически m и р – взаимно просты.

Допустим если а вне диапазона (a>m),

если а и m – взаимно просты то будет справедливо и для этого случая.

А если m – простое(р), то а не должно делится на р. Т.е. если а делится на р, то это уже не соответствует определению взаимно простых чисел.

Дата добавления: 2014-01-15