Получение простых чисел

По мере того как мы будем изучать курс «Математические основы криптологии» мы будем возвращаться к этой теме.

Задача получение простых чисел во многом зависит от того как ставить эту задачу.

Методы:

1)Разложение. Самый древний способ получения простых чисел, как мы уже знаем, - решето Эратосфена. но максимум получение чисел на современной вычислительной технике по этому способу, это N=10¹².

2) Формульный метод. С помощью формул можно получить некоторое множество чисел, но оно ограниченно. Простейшие:

а) целочисленные полиномы (в общем случае не решают задачу получение бесконечного множества простых чисел.)

б) экспоненциальная функция. (множество получаемое на основе данного способа, как мы уже говорили, ограничено по мощности.

этот способ имеет больший интерес для анализа криптошифра.

в) прамориальная формула. Пока не известно можно ли по этой формуле получить бесконечное число простых чисел.

3. Тестирование.

Задано некоторое число m и проверяется по определенному алгоритму, является ли оно простым. Так называемое тестирование на простоту. Этот способ используется в современных криптографических системах с открытым ключём. Берется некоторое большое число (сотни десятичных знаков) и по отношению к этому числу начинается тестирование.

Существует 2 метода тестирования на простоту:

1)строгие тесты(детерминированные).

отвечают на вопрос простое или составное однозначно.

2)вероятностные тесты. С помощью них мы можем говорить только с некоторой вероятностью, что данное число простое. При этом вероятность может быть сколь угодна близка к единице. Но эти методы гораздо быстрее, нежели строгие, по отношению к большим числам. Т.е. когда информация не столь важна(для шифрование) мы можем рискнуть, и с некоторой вероятностью, использовать вместо простого числа составное.

Метод, объединяющий в себе как вероятностные, так и детерминированные методы называется комбинированным методом. Т.е. сначала мы выясняем, с некоторой вероятностью, что число m простое и потом по отношению к нему применяем строгий метод и в итоге это более оптимально чем сразу применять к некоторому большому числу строгий тест.

С понятием «строгие тесты» связанно такое понятие как «факторизация».

Факторизация – разложение заданного числа на простые сомножители.

Одним из первых методов факторизации является метод разложение чисел Мерсена [M(p)]. Еще в 19 веке был предложен тест проверки чисел Мерсена на простоту. Это был один из первых строгих тестов.

Так как же определить является ли число Мерсена простым или составным? Существует метод, причем достаточно эффективный для больших чисел.

Тестирование чисел Мерсена М(р)

Рассмотрим алгоритм.

(строгий тест)

Дано число Мерсена. М(р)

1. Получаем последовательность определенных целых чисел S₁,S₂,…S_p-2 Получаем ее по правилу S_i+1=S_i²-2. Т.е. каждый последующий член последовательности равен квадрату предыдущего минус 2.

Но при этом задается S₀=4. Тогда при р=5:М(р)=31S₀=4 S₁=14, S₂=(14²-2)²-2. Казалось бы идет быстрое нарастание чисел, что представляет определенную сложность для дальнейших вычислений, но в Теории чисел есть определенные «хитрости» которые мы рассмотрим в дальнейшем.

2. Тестируем S_p-2 по формуле:

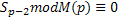, если 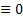то число простое (т.е. без остатка)

если в остатке есть некоторое число, то число составное. Причем остаток меньше чем М(р).

Вопрос заключается в том, как можно эффективно реализовать эту операцию при больших числах Мерсена. Ответ на этот вопрос существует, но сейчас нам сложно его объяснить, рассмотрим эту модульную операцию в последующих лекциях. На этой операции буквально и держится вся криптография. Она применяется по отношению к определенным функциям. Почти все известные методы тестирования тоже основаны на этой операции. Как современные так и древние. Какими свойствами обладает эта операция и ее приложение, мы посветим этому несколько лекций позднее.

Рассмотрим алгоритм факторизации (алгоритм Ферма).

Задано число, мы пытаемся его разложить. Если раскладывается, то составное, если нет, то простое.

Тоже определенная форма строгого теста.

1) Задано число m, причем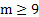

m=m₀

m₁=m₀+1

m₂=m₁+3

m₃=m₂+5

…………

m_i=m_i-1+2i-1

Возникает вопрос: Бесконечно ли можно продолжать этот ряд. Ответ: Нет.

С каждым членом (m_i) проводим следующую операцию. Можно ли его представить в виде квадрата некоторого числа.

m_i=t²

Если можно то мы останавливаем процесс и

m= (t-i)(t+i) и причем (t-i) – это p₁,а p₂= (t+i), где p₁ и p₂ - простые сомножители.

Пример:

m=391=m₀

m₁=391+1;

m₂=392+3;

m₃=395+5 =400= t²=20;

m=391=(20-3)(20+3) т.е. p₁=17 и p₂=23;

Но этот алгоритм действует только до определенных границ:

Ограничение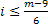

Если исходное число велико, то это сокращает число членов в 6 раз. Если рассмотреть на оси точки которые является квадратами некоторых чисел, то число квадратов гораздо больше чем число простых чисел и на квадраты мы натыкаемся гораздо быстрее.

Если до величины 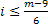мы не нашли квадрата, то мы останавливаемся.

Дата добавления: 2014-01-15