При последовательном нахождение всех простых чисел, на оси натуральных чисел, 1,2,3,5…N то при таком способе достаточно рассмотреть (дойти до) простое число

Т.е. этого достаточно, чтобы при таком последовательном способе получить все простые числа на этой оси. Примером данного способа является Решето Эратосфена.

4) Если мы имеем произведение двух натуральных чисел a*b и имеем простое число p, причем такое что p|a*b, тогда p|a или p|b. (это свойство играет не последнюю роль при анализе криптоалгоритмов)

Эти свойства используются в теории делимости целых чисел.

А теперь выясним в чем заключается сложность получения разложения. Если мы посмотрим на оси как расположены простые числа, то выясним что оказывается до сих пор не найдена закономерность их расположения. С одной стороны они расположены не случайно, а с другой стороны не найдено формулы с помощью которой можно было бы получить всю последовательность таких чисел.

Последовательность простых чисел бесконечна. Это доказано еще Евклидом. Пытались выразить последовательность простых чисел с помощью целочисленных полиномов, но было доказано еще в 19 веке что с их помощью нельзя получить всю бесконечную последовательность чисел. Отдельные подмножества этой последовательности получить можно. н-р: x²-30+40. если иксу предавать значения 1, 2,3…40, то получим 40 простых чисел. Есть формулы которые дают большие по мощности подмножества, но все-таки это отдельные подмножества.

Теперь рассмотрим порядок расположения простых чисел. Все таки какие-то закономерности есть, ряд так называемых асимптотических закономерностей:

1) Плотность появления простых чисел на заданном интервале падает с увеличением N.

Н-р: при N=10 у нас 4 простых числа (от 1 до 10) (40%)

при N=100 имеем 25 чисел (1 до 100) (25%)

при N=1000 около 13%

и так далее плотность убывает. Тем не менее интервалы расположение таких чисел совершенно не предсказуемы. Есть числа расположенные близко к друг другу (5,7; 11,13; 13,19 – простые числа близнецы). Причем до сих пор не доказано бесконечно ли число близнецов или нет.

Допустим задан интервал и мы хотим оценить плотность в заданном интервале (от 1 до N). Плотность определяется по формуле: - асимптотическая плотность. Это отношение начинает хорошо проявляться при больших N. С ростом N эта величина растет.

Зафиксируем некоторый интервал на оси от 1 до N. потом прибавим некоторое 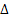. И вот в зависимости от величины 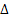существуют оценки, сколько простых чисел в интервале N+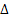. Проблема заключалось в том чтобы узнать величину этого интервала чтобы в нем находилось хотя бы одно простое число. Еще в 18 веке была получена 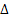(потом она конечно уточнялась). На сегодняшний день эта 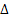имеет величину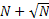

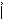
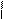
N N 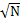- на этом интервале гарантированно есть хотя бы одно

простое число.

Это свойство тоже является не последним по важности для криптоаналитиков.

В попытках открыть закономерность расположения простых чисел ученные выяснили седующие:

Допустим мы имеем простое число 11 оно состоит из двух единиц.

рассмотрим простые числа построенные из единиц. Выясним какое ближайшее простое число состоит тоже только из единиц. 111 – не простое число. 1111- тоже не простое. Числа составленные из трех до восемнадцати единиц не являются простыми. А вот число 1111111111111111111 – простое (состоит из 19 единиц). Это так называемое второе простое число.

Третье это - 11111111111111111111111 (23 единицы).

А вот четвертое простое число до сих пор ищется. Уже перебрали числа состоящие из 70 единиц но пока не нашли простого числа.

Т.е имеются определенные «сгустки» простых чисел на оси которые дают интересные формулы,

(допустим если расположить простые числа на шахматной доске, то они будут стоять по диагонали) но в целом одну формулу для всех пока не нашли.

Одна из проблемных задач которой занимались начиная с Ферма, позднее Эйлер, Гаусс ….

как раскладывать составное число. Допустим школьный метод проб. Проверяем сначала делится ли на 2,3….. Он не используется в шифрование из за своей очевидности.

Пример:

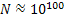исходя из этого числа нам нужно перебрать все делители, чтобы последний был

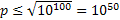– если мы не нашли делителей до этого числа то простое.

Но чтобы найти делители в этом интервале (на среднем компьютере) нам понадобится 10⁴⁰секунд. 10⁸ – то примерное количество секунд в одном годе. т.е. понадобится 10³² лет чтобы найти все делители.

Для справки: Большой Взрыв, приведший к зарождению вселенной, произошел примерно 10¹¹ лет тому назад. Даже если мы возьмем 1000 000 000 компьютеров то нам понадобится 10²⁵ лет.

В перспективе, на квантовых компьютерах этот алгоритм не будет являться проблемой.

Существуют определенные алгоритмы которые ускоряют нахождение простых делителей, но опять таки это зависит от диапазоны в котором мы пытаемся их найти. Еще Ферма предложил определенный алгоритм. Мы рассмотрим его модификацию чуть позже. Он предназначен для случаев когда число m имеет хотя бы один небольшой делитель. Не больше чем корень из N.

Составные числа могут иметь запись не только в виде канонического разложения, но и в виде определенной формулы. Например: простейший полином (один из интереснейших в современной криптографии). Дано некоторое число, причем не известно какое оно простое или составное.

и оно имеет в запись вид:

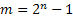– полином степени n, где в качестве х выступает 2-ка.

Установлена определенная закономерность что если n четное то m всегда является составным.

Если n нечетное, но составное тогда число m тоже составное. Но если n нечетное, но простое, то при некоторых простых n число m составное, а при некоторых простое. Т.е, или/или. Начиная с 17 века эта формула изучается. В криптографии имеет интересную роль, что это один из простых способов получения простых чисел. Берем большое n – простое, и потом тестируем, полученное m может оказаться или простым или составным. Простые числа получаемые при n простых расположены на оси редкими группами. Впервые эту закономерность начал изучать Мерсен (18 век). Он быль не столько математик, сколько любитель математик. Он начал подставлять в n 2,3,5,7…. и он получил ряд чисел (до тех пор пока ему было легко это делать на бумаге). Так он дошел до n=257, но он ошибся, 257 – не простое число. Подставляя, он получил ряд(причем в нем он допустил ряд ошибок), который выглядит следующим образом:

n= 2,3,5,7,13,17,19,31,67,127,157 т.е. те простые числа, при подставление которых в формулу 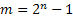получаем простое число.

Ошибки;

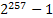- составное

-составное

он пропустил числа 41,47,61,89 и надо убрать 67 и 257.

Самое большое простое число найдено при n = 3021377

само это простое число, содержит 1819050 десятичных знаков.

Способы возведение в большую степень рассмотрим позже.

Ферма выдвинул предположение, что число - является простым. Но при k =5 – число получается составное. А при k=0,1,2,3,4. И до сих пор не найдено простого числа после k=5.

Предыдущие формулы являлись экспоненциальными, но существует еще одна интересная формула:

Праимориальная формула. Из школы нам известно понятие факториал. Он определяется как 1*2*3*4*…..*N. А прамориал - берется простое число p и на основе его составляется прамориальная формула такого типа: произведение простых сомножителей до p(включая p). 2*3*5*7*…*p. прамориал обозначается - p#.

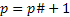- полученное число может быть как составным так и простым. Эта формула так до конца и не исследована.Но она тоже быстро иссекает. Но основе этого понятия (прамориал) следует одно из возможных доказательств, которое было использовано еще Евклидом, бесконечности простых чисел.

Дата добавления: 2014-01-15