Алгоритмы поиска больших простых чисел

Простым называется целое число, больше единицы, единственными множителями которого является 1 и оно само: оно не делится ни на одно другое число. Например, простыми являются 73, 2521, 2365347734339 и 2⁷⁵⁶⁸³⁹–1. Вся криптография с открытыми ключами основана на том факте, что существует бесконечно много простых чисел (Теорема Эвклида). В реальной криптографии используются большие простые числа, размер которых 512 бит и более.

Существует приблизительно 10¹⁵¹ простых чисел длиной 512 бит.

Для чисел, близких n, вероятность того, что случайно выбранное число окажется простым равна 1/ln(n ). Полное число простых чисел меньших n, приблизительно равно n/ ln(n).

Может ли случится, что два человека слдучайно выберут одно и то же простое число? Из 10¹⁵¹ простых чисел вероятность совпадения выбора значительно меньше, чем вероятность того, что в ваш компьютер ударит молния в тот момент когда вы выиграете в лотерею самый престижный приз.

Если кто-то создаст базу данных всех простых чисел, может сможет он ее использовать для вскрытия алгоритмов с открытыми ключами? Пусть мы будем хранить один гигабайт информации на устройстве, весящем 1 грамм, то перечень простых чисел размерос до 512 бит имел такую массу, что она превысила бы предел Чандрасе́кара. Наша флэшка бы сколлапсировала бы в черную дыру и извлечь откуда данные все равно будет невозможно.

Преде́л Чандрасе́кара — это верхний предел массы, при котором звезда может существовать как белый карлик. Если масса звезды превышает этот предел, то она становится нейтронной звездой.

Алгоритмы поиска больших простых чисел можно разделить на две группы: алгоритмы перебора и вероятностные алгоритмы. К первой группе относятся алгоритм прямого перебора с проверкой делимости и «решето Эратосфена». Такие алгоритмы неэффективны для больших чисел, поскольку работают очень медленно. Вторая группа алгоритмов использует вероятностные оценки для определения простоты числа. Наиболее широкое распространение получили алгоритм Рабина-Миллера и тест Лемана [8].

Алгоритм был разработан Гари Миллером в 1976 году и модифицирован Майклом Рабином в 1980 году

Алгоритм Рабина Миллера предлагает следующую схему генерации простого числа:

1. Выберите для проверки случайное число p. Вычислите b – число делений p – 1 на 2 (2 b – это наибольшая степень числа 2, на которое делится
p – 1). Затем вычислите m, такое что p = 1 + 2 b * m.

2. Выберите случайное число a < p.

3. Установите j = 0 и вычислить z = a×m mod p.

4. Если z = 1 или z = p – 1, то p проходит проверку и может быть

простым числом.

5. Если j > 0 и z = 1, то p не является простым числом.

6. Установите j = j + 1. Если j < b и z 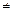p – 1, установите z = 2 z mod p и

вернитесь к пункту 4. Если z = p – 1, то p проходит проверку и может

быть простым числом.

7. Если j = b и z 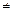p – 1, то p не является простым числом.

Число окажется составным через t проверок с вероятностью не большей (1/4) ^t , где t – это число итераций.

Альтернативный алгоритм для поиска простых чисел был разработан Леманом.

Вот последовательность действий при проверке простоты числа p:

1. Выбрать случайное число а, причем a<p;

2. Вычислить k= a^{(p-1) div2}mod p;

3. Если k ≠ 1 или k≠ (p-1), то рассматриваемое p не является простым.

4. Если k =1 или k= (p-1), то вероятность того, что p не является простым, не более 50 процентов.

5. Попытку (1) – (4) повторить т раз с различными случайными значениями a.

Если результат вычислений равен 1 или (p –1), но не всегда равен 1, то p является простым числом с вероятностью ошибки 1/2 ^m.

Два числа называются взаимно простыми, если у них нет общих множителей кроме 1. Иными словами, если наибольший общий делитель этих чисел равен 1. Если n является простым числом, то любое число от 1 до n –1 взаимно просто с n. Взаимно просты числа 15 и 32, 27 и 64. Одним из способов вычислить наибольший общий делитель двух чисел является алгоритм Эвклида, описанный в книге Элементы (300 год до н. э.)

Дата добавления: 2014-01-15